题目内容
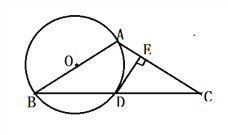
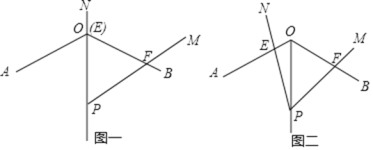
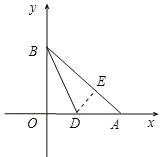
【题目】如图1,在平面直角坐标系xOy中,A(a,0)、B(0,b)、C(﹣a,0),且![]() +b2﹣4b+4=0
+b2﹣4b+4=0
(1)求证:∠ABC=90°;
(2)作∠ABO的平分线交x轴于一点D,求D点的坐标;
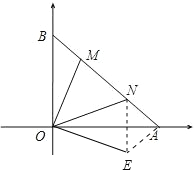
(3)如图2所示,A、B两点在x轴、y轴上的位置不变,在线段AB上有两动点M、N,满足∠MON=45°,下列结论:①BM+AN=MN;②BM2+AN2=MN2,其中有且只有一个结论成立.请你判断哪一个结论成立,并证明成立的结论.

【答案】(1) 证明见解析;(2)D(![]() ,0);(3) ②是对的(基本结论),证明见解析.
,0);(3) ②是对的(基本结论),证明见解析.
【解析】
试题(1)由![]() 可得a=2,b=2,即可得A、B、C的坐标,即可判定∠ABC=90°;(2) 过D作DE⊥AB于E,由于BD是∠ABO的角平分线,根据角平分线的性质知DO=DE,设OD=x,根据S△AOB的两种求法列出方程,由此求出OD的长,从而得到D点的坐标.(3)此题要通过构造全等三角形来求解;作OE⊥OM,且使得OE=OM,由于∠MON=45°,那么∠EON=∠MON=45°,即可证得△MON≌△EON,MN=NE;同理可通过证△MON≌△EON,来得到BM=AN,∠OAE=∠OBM=45°,因此在Rt△NAE中,根据勾股定理即可证得(2)的结论是正确的.
可得a=2,b=2,即可得A、B、C的坐标,即可判定∠ABC=90°;(2) 过D作DE⊥AB于E,由于BD是∠ABO的角平分线,根据角平分线的性质知DO=DE,设OD=x,根据S△AOB的两种求法列出方程,由此求出OD的长,从而得到D点的坐标.(3)此题要通过构造全等三角形来求解;作OE⊥OM,且使得OE=OM,由于∠MON=45°,那么∠EON=∠MON=45°,即可证得△MON≌△EON,MN=NE;同理可通过证△MON≌△EON,来得到BM=AN,∠OAE=∠OBM=45°,因此在Rt△NAE中,根据勾股定理即可证得(2)的结论是正确的.
试题解析:
证明:∵![]()
∴a=2,b=2,
∴A(2,0)、B(0,2)、C(-2,0),
∴△AOB和△COD是等腰直角三角形,
∴∠ABC=90°
(2) 过点D作DE⊥AB于E
∵BD平分∠ABO
∴OD=DE
设OD=x
∵S△AOB=![]() ×2×2=
×2×2=![]() ×2×x+
×2×x+![]() ×
×![]() ×x,解得
×x,解得![]()
∴D(![]() ,0)
,0)
(3) ②是对的(基本结论).
过点O作OE⊥OM,并使OE=OM,
在△MOB和△EOA中,
OB=OA,∠MOB=∠AOE,OM=OE,
∴△MOB≌△EOA,
∴BM=AE,∠B=∠OAE,
在△MON和△EON中,
OM=OE,∠MON=∠NOE=45°,ON=ON,
∴△MON≌△EON;
∴MN=NE,
又∵∠NAE=∠NAO+∠OAE=90°,
∴△NAE为直角三角形,
∴NA2+AE2=NE2
∴BM2+AN2=MN2,即结论②正确.

【题目】某校学生会文艺部换届选举,经初选、复选后,共有甲、乙、丙三人进入最后的竞选.最后决定利用投票的方式对三人进行选举,共发出1800张选票,得票数最高者为当选人,且废票不计入任何一位候选人的得票数内,全校设有四个投票箱,目前第一、第二、第三投票箱已开完所有选票,剩下第四投票箱尚未开箱,结果如表所示(单位:票):
投票箱 | 候选人 | 废票 | 合计 | ||
甲 | 乙 | 丙 | |||
一 | 200 | 211 | 147 | 12 | 570 |
二 | 286 | 85 | 244 | 15 | 630 |
三 | 97 | 41 | 205 | 7 | 350 |
四 | 250 | ||||
下列判断正确的是( )
A. 甲可能当选 B. 乙可能当选 C. 丙一定当选 D. 甲、乙、丙三人都可能当选