��Ŀ����
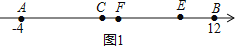
����Ŀ��������A��B�����Ӧ�����ֱ��ǩ�4��12���߶�CE���������˶�����C�ڵ�E����ߣ���CE��8����F��AE���е㣮
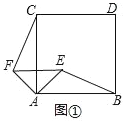
��1����ͼ1�����߶�CE�˶�����C��E����A��B֮��ʱ����CF��1����AB�� ��AC�� ��BE�� ��


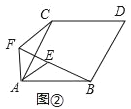
��2�����߶�CE�˶�����A��C��E֮��ʱ,
����AF��Ϊ![]() ���ú�
���ú�![]() �Ĵ���ʽ��ʾBE�� ������軯������
�Ĵ���ʽ��ʾBE�� ������軯������
����BE��CF��������ϵ��
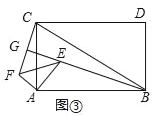
��3������C�˶��������ϱ�ʾ����14��λ��ʱ������P�ӵ�E��������ÿ��3����λ���ȵ��ٶ������˶����ִ�B��������ԭ��һ���ٶȷ��أ�ͬʱ��Q��A��������ÿ��2����λ���ȵ��ٶ����յ�B�˶����������˶���ʱ��Ϊt�루t��8������tΪ��ֵʱ��P��Q�����ľ���Ϊ1����λ���ȣ�
���𰸡���1��16,6,2����2����![]() ��
��![]() ����3��t=1��3��
����3��t=1��3��![]() ��
��![]()
��������
(1)��������A��B�����Ӧ�����քe��-4��12���ɵ�AB�ij�;��CE��8��CF��1���ɵ�EF�ij����ɵ�F��AE���е㣬�ɵ�AF�ij�����AB�ij���ȥ2����EF�ij���ΪBE�ij���
(2)��AF��FE��x����CF��8-x���ú�x��ʽ�ӱ�ʾ��BE�����ɵó���
(3)�֢ٵ�0��t��6ʱ�� �ڵ�6��t��8ʱ������������ۼ��㼴�ɵý�
��1��������A��B�����Ӧ�����ֱ���-4��12��
��AB=16��
��CE=8��CF=1����EF=7��
�ߵ�F��AE���е㣬��AF=EF=7��
,��AC=AF��CF=6��BE=AB��AE=16��7��2=2��
�ʴ�Ϊ16��6��2��
(2)�ߵ�F��AE���е㣬��AF=EF��
��AF=EF=x,��CF=8��x��
��BE=16��2x=2��8��x����
��BE=2CF.
�ʴ�Ϊ��![]() ��
��![]() ��
��
(3) �ٵ�0��t��6ʱ��P��Ӧ����-6+3t��Q��Ӧ��-4+2t��
![]() ��
��
��ã�t=1��3��
�ڵ�6��t��8ʱ��P��Ӧ��![]() �� Q��Ӧ��-4+2t��
�� Q��Ӧ��-4+2t��
![]() ��
��
��ã�![]() ��
��![]() ��
��
�ʴ�Ϊt=1��3��![]() ��
��![]() .
.

 ��У����ϵ�д�
��У����ϵ�д�