题目内容
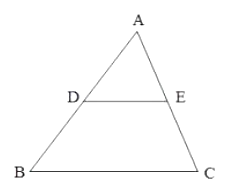
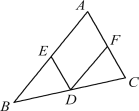
【题目】如图,点D,E,F分别是△ABC三边的中点,则下列判断错误的是( )
A. 四边形AEDF一定是平行四边形 B. 若AD平分∠A,则四边形AEDF是正方形
C. 若AD⊥BC,则四边形AEDF是菱形 D. 若∠A=90°,则四边形AEDF是矩形
【答案】B
【解析】
一组对边平行且相等的四边形是平行四边形;有一个角是直角的平行四边形是矩形;对角线互相垂直的平行四边形是菱形.
A.∵点D. E.F分别是△ABC三边的中点,∴DE、DF为△ABC得中位线,
∴ED∥AC,且ED=![]() AC=AF,同理DF∥AB,且DF=
AC=AF,同理DF∥AB,且DF=![]() AB=AE,
AB=AE,
∴四边形AEDF一定是平行四边形,正确;
B. 若AD平分∠A,延长AD到M,使DM=AD,连接CM,由于BD=CD,DM=AD,
∠ADB=∠CDB,(SAS)∴△ABD≌△MCD∴CM=AB,又∵∠DAB=∠CAD,
∠DAB=∠CMD,∴∠CMD=∠CAD,∴CA=CM=AB,因AD平分∠A
∴AD⊥BC,则△ABD≌△ACD;AB=AC,AE=AF,
结合A选项所以四边形AEDF是菱形,因为∠A不一定是直角
∴不能判定四边形AEDF是正方形;
C. 若AD⊥BC,则△ABD≌△ACD;AB=AC,AE=AF,结合A选项所以四边形AEDF是菱形,正确;
D. 若∠A=90°,则四边形AEDF是矩形,正确.
故答案选B.

练习册系列答案
相关题目