Question

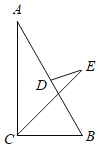
【题目】如图，△ABC中，∠ACB＝90°，∠B＝60°，AB＝4，D为AB中点，CE平分∠ACB，∠DEC＝30°，则CE＝_____．

Answer 1

【答案】2

【解析】

连接CD，作CH⊥DE于H，由直角三角形的性质可得CD＝BD＝AD＝2，∠A＝30°，可得HD＝HC＝，由直角三角形的性质可得CE＝2HC＝2．

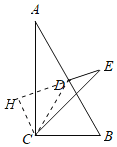
解：连接CD，作CH⊥DE于H

∵∠ACB＝90°，∠B＝60°，AB＝4，D为AB中点，

∴CD＝BD＝AD＝2，∠A=90°-60°＝30°，

∴∠ACD＝∠A＝30°，

∵CE平分∠ACB，

∴∠ACE＝45°，

∴∠DCE＝15°，

∴∠HDC＝∠DEC+∠DCE＝45°，且CH⊥DE，

∴∠HCD＝∠HDC＝45°，且CD＝2，

∴HD＝HC=sin∠HDC·CH＝．

∵∠DEC＝30°，CH⊥DE，

∴CE＝2CH＝2．

故答案为：2．