��Ŀ����
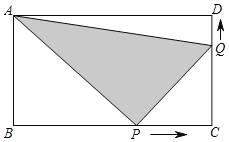
����Ŀ����ͼ��ֱ��y��![]() x+6��x�ᡢy�ύ��A��B���㣬��C�ڵ������ޣ�BC��AB����BC��AB��
x+6��x�ᡢy�ύ��A��B���㣬��C�ڵ������ޣ�BC��AB����BC��AB��
��1����ͼ1�����C�����ꣻ
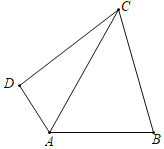
��2����ͼ2��D��BC���е㣬��D��AC�Ĵ���EF��AC��E����ֱ��AB��F������CF����PΪ����AD��һ���㣬��PF2��PC2��ֵ��
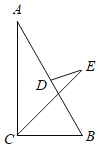
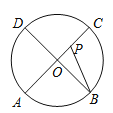
��3����ͼ3���ڣ�2���������£��ڵڶ�������A���߶�AM��AB�ڵ�A�����߶�AB��ȡһ��N������MN��ʹMN��BN���ڵ�������ȡһ��Q��ʹ��NMQ��90��������QC����QC��AB����QC��6AM�����P�ĺ�����Ϊt����PMQ�����Ϊs����s��t�ĺ�����ϵʽ��

���𰸡���1��C(6����2)����2��25����3��![]()
��������
��1����C��CH��y����H������BCH+��CBH��90����֤����BHC�ա�AOB��AAS�����ɽ�����⣻
��2����ͼ2�У�������AD��CF��G�����ݡ�SAS��֤����ABD�ա�CBF�����ù��ɶ���������⼴�ɣ�
��3����ͼ3�У�����BM��BQ����B��BK��QM�ӳ����ڵ�K���ӳ�MA��QC�ڵ�T���ɵ�������ABCT��֤����BKM�ա�BAM��ASA�����Ƴ�BA��BK��BC��MK��MA��֤��Rt��BKQ��Rt��BCQ��HL�����Ƴ�QK��QC����AM��a����QK��QC��6a����Rt��QMT�У�MQ��5a��MT��a+10��QT��6a��10�����ɶ����ɵ�a��![]() ����tan��MNA��tan��QMT��tan��BAO��
����tan��MNA��tan��QMT��tan��BAO��![]() ���Ƴ�QT��10��MQ��
���Ƴ�QT��10��MQ��![]() ��MT��
��MT��![]() ����PS��MQ�ڵ�S������
����PS��MQ�ڵ�S������![]() �����㼴�ɣ�
�����㼴�ɣ�
�⣺��1����ͼ1�У�
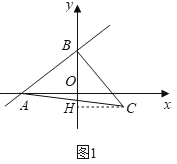
��y��![]() x+6����y��0����x����8����x��0����y��6
x+6����y��0����x����8����x��0����y��6
��A(��8��0)��B(0��6)��
��OA��8��OB��6��
��C��CH��y����H������BCH+��CBH��90����
��BC��AB��
���ABO+��CBH��90����
���BCH����ABO��
����BHC����AOB��90����BC��AB��
���BHC�ա�AOB��AAS����
��HC��OB��6��BH��OA��8��OH��8��6��2��
��C(6����2)��
��2����ͼ2�У�������AD��CF��G��
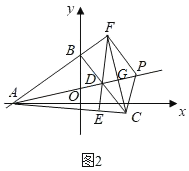
��BC��AB��BC��AB��
���BAC��45��
��EF��AC��
���AFE��45��
���BDF�ǵ���ֱ�������Σ�
��BD��BF��
����ABD����CBF��90����AB��CB
���ABD�ա�CBF��SAS����
���BAD����BCF��
�ߡ�BDA����CDG��
���CGD����ABD��90����
��AD��CF��
��OA��8��OB��6��
��AB��![]() ��10��
��10��
��BC��10��
��BF��BD��5��
��PF2��PC2��(PG2+FG2)��(PG2+CG2)
��FG2��CG2��(DF2��DG2)��(DC2��DG2)
��DF2��DC2��DF2��BD2��BF2��25
��3����ͼ3�У�����BM��BQ����B��BK��QM�ӳ����ڵ�K���ӳ�MA��QC�ڵ�T���ɵ�������ABCT��
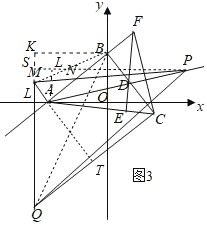
��MN��BN��
���NMB����NBM��
��BK��QK��NM��QK��
��BK��MN��
���KBM����BMN��
���KBM����MBA��
��MB��MB����K����BAM��90��
���BKM�ա�BAM��ASA����
��BA��BK��BC��MK��MA��
��Rt��BKQ��Rt��BCQ��HL����
��QK��QC��
��AM��a����QK��QC��6a��
��Rt��QMT�У�MQ��5a��MT��a+10��QT��6a��10�����ɶ����ɵ�a��![]() ��
��
��tan��MNA��tan��QMT��tan��BAO��![]() ��
��
��QT��10��MQ��![]() ��MT��
��MT��![]()
��MN��x�ᣬMQ��y�ᣬ��PS��MQ�ڵ�S��
��![]() ��
��
��MQ��x�ύ�ڵ�I��Rt��MAI�У�AI��2��
��AL��PS�ڵ�L���þ���ALSI��
��PS��PL+LS��t+10��
��![]() ��
��
��![]() ��
��

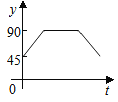
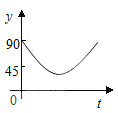
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�