题目内容
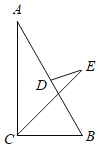
【题目】如图,在矩形ABCD中,AB=4,BC=6,点M是BC的中点.
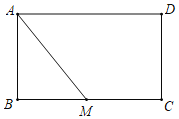
(1)在AM上求作一点E,使△ADE∽△MAB(尺规作图,不写作法);
(2)在(1)的条件下,求AE的长.
【答案】(1)过D 作DE⊥AM于E,△ADE即为所求;见解析;(2)AE=![]() .
.
【解析】
(1)根据题意作出图形即可;
(2)先根据矩形的性质,得到AD∥BC,则∠DAE=∠AMB,又由∠DEA=∠B,根据有两角对应相等的两三角形相似,即可证明出△DAE∽△AMB,根据相似三角形的对应边成比例,即可求出DE的长,根据勾股定理即可得到结论.
解:(1)过D 作DE⊥AM于E,△ADE即为所求;
(2)∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DAE=∠AMB,
又∵∠DEA=∠B=90°,
∴△DAE∽△AMB,
∴DE:AD=AB:AM,
∵M是边BC的中点,BC=6,
∴BM=3,
又∵AB=4,∠B=90°,
∴AM=5,
∴DE:6=4:5,
∴DE=![]() ,
,
∴AE=![]() =
=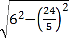 =
=![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】云南边防部队在戍边卫国的艰辛历程中,为祖国和人民建立了不可磨灭的功勋.为保障边防部队的生活,现从甲、乙两个仓库向A、B两军营运送生活物资,已知甲仓库可调出生活物资100吨,乙仓库可调出生活物资80吨;A军营需生活物资70吨,B军营需生活物资110吨,两仓库到A、B两军营的路程和运费如下表:
路程(千米) | 运费(元/吨·千米) | |||
甲仓库 | 乙仓库 | 甲仓库 | 乙仓库 | |
A军营 | 20 | 15 | 12 | 12 |
B军营 | 25 | 20 | 10 | 8 |
设甲仓库运往A军营生活物资为x吨(x为整数),总运费为y(元).
(1)求y与x的函数解析式(也称关系式),并直接写出x的取值范围;
(2)若要使总运费不超过37160元,有几种运送生活物资方案?哪种运送方案总运费最少?