Question

【题目】如图，△ABC为等腰直角三角形，∠ABC=90°,过点B作BQ∥AC,在BQ上取一点D，连接CD、AD,若AC=CD,BD=,则 AD=_______________．

Answer 1

【答案】2

【解析】如图所示,

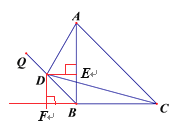
过点D作DE⊥AB,DF垂直CB的延长线于点F,

因为BQ∥AC,所以∠ABD＝∠BAC=45°,

在Rt△BED中,BD=, ∠ABD =45°,所以DE=BD=,即BF=1,

设BC=x,根据勾股定理可得:AC=x,所以CD=x,

在Rt△DFC中,根据勾股定理可得: ,解得x=1+, x=1-,

所以AE= ,

在Rt△DEA中,根据勾股定理可得:AD=2,

故答案为:2.

点睛:本题主要考查解直角三角形和勾股定理,解决本题的关键是要熟练掌握解直角三角形的方法.