Question

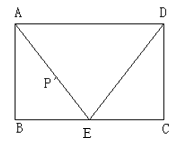
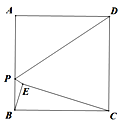
【题目】如图，正方形ABCD的边长为6，点E是正方形内部一点，连接BE，CE，且∠ABE=∠BCE，点P是边AB上一动点，连接PD，PE，则PD+PE的最小值为_____.

Answer 1

【答案】

【解析】

根据正方形的性质得到∠ABC＝90°，推出∠BEC＝90°，得到点E在以BC为直径的半圆上移动，如图，设BC的中点为O，作正方形ABCD关于直线AB对称的正方形AFGB，则点D的对应点是F，连接FO交AB于P，交⊙O于E，则线段EF的长即为PD+PE的长度最小值，根据勾股定理即可得到结论．

解：∵四边形ABCD是正方形，

∴∠ABC＝90°，

∴∠ABE+∠CBE＝90°，

∵∠ABE＝∠BCE，

∴∠BCE+∠CBE＝90°，

∴∠BEC＝90°，

∴点E在以BC为直径的半圆上移动，

如图，设BC的中点为O，

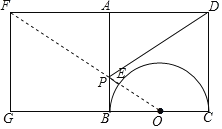
作正方形ABCD关于直线AB对称的正方形AFGB，

则点D的对应点是F，

连接FO交AB于P，交半圆O于E，

则线段EF的长即为PD+PE的长度最小值，

∵∠G＝90°，FG＝BG＝AB＝6，

∴OG＝9，

∴OF＝＝，

∴EF＝，

故PD+PE的长度最小值为，

故答案为：．