Question

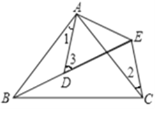
【题目】如图，己知AB是⊙O 的直径，C是⊙O 上一点，∠ACB的平分线交⊙O 于点D，作PD∥AB，交CA的延长线于点P．连结AD，BD．

求证：（1）PD是⊙O 的切线；

（2）△PAD△DBC.

Answer 1

【答案】见解析

【解析】（1）根据角平分线的定义得出∠1=∠3，得出弧AD=弧BD，根据垂径定理可得出OD⊥AB，再根据PD∥AB，就可证得OD⊥PD，即可得证；

（2）根据圆内接四边形的定理，可证得∠2=∠CBD，再根据圆周角定理及等腰直角三角形的性质，可证得∠ADP=∠1，然后根据相似三角形的判定定理，可证得结论.

（1）证明：如图，连接OD

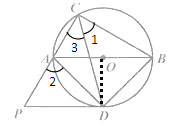
∵CD平分∠ACB

∴∠1=∠3

∴弧AD=弧BD

∴OD⊥AB

∵PD∥AB

∴OD⊥PD

∵OD是半径

∴PD是⊙O的切线

（2）证明：∵四边形ADBC是圆的内接四边形，

∴∠CAD+∠CBD=180°

∵∠2+∠CAD=180°

∴∠2=∠CBD

∵AB是圆的直径

∴∠ADO+∠BDO=90°，∠1+∠3=90°，即∠1=45°

∵弧AD=弧BD，OD⊥AB

∴AD=BD

∴∠ADO=45°

∵∠ADO+∠ADP=90°

∴∠ADP=45°=∠1

∴△PAD∽△DBC