��Ŀ����
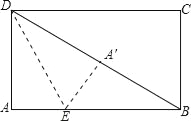
����Ŀ����ͼ1�����ı���ABCD�У�AB=AD. ��B+��ADC=180�㣬��E��F�ֱ����ı���ABCD�ı�BC��CD�ϣ���EAF=![]() ��BAD������EF���Բ���EF��BE��DF֮���������ϵ.
��BAD������EF���Բ���EF��BE��DF֮���������ϵ.

ͼ1 ͼ2 ͼ3
(1)˼·����
����ABE�Ƶ�A��ʱ����ת����ADG��ʹAB��AD�غ�.�ɡ�B+��ADC=180�㣬�á�FDG=180�㣬����F��D��G���㹲��. ��֤��AFG![]() ����EF��BE��DF֮���������ϵΪ ��
����EF��BE��DF֮���������ϵΪ ��
(2)�������
��ͼ2����ͼ1�������£�����E��F��ԭ����λ�÷ֱ�䵽�ı���ABCD�ı�CB��DC���ӳ����ϣ���EAF=![]() ��BAD������EF���Բ���EF��BE��DF֮���������ϵ��������֤��.
��BAD������EF���Բ���EF��BE��DF֮���������ϵ��������֤��.
(3)������չ
��ͼ3���ڡ�ABC�У���BAC=90�㣬AB=AC����D��E���ڱ�BC�ϣ��ҡ�DAE=45��. ��BD=1��EC=2����DE�ij�Ϊ .
���𰸡���1����AFE. EF=BE+DF.��2��BF=DF-BE�����ɼ���������3��![]()
�������������������1���ȸ�����ת�ã� ![]() ����
����![]() ����
����![]() ���ߣ��ٸ���SAS֤����AFE�ա�AFG����EF=FG���ɵý���EF=DF+DG=DF+AE��
���ߣ��ٸ���SAS֤����AFE�ա�AFG����EF=FG���ɵý���EF=DF+DG=DF+AE��
��2����ͼ2��ͬ���������ߣ��ѡ�ABE�Ƶ�A��ʱ����ת![]() ����ADG��֤����EAF�ա�GAF����EF=FG������EF=DFDG=DFBE;
����ADG��֤����EAF�ա�GAF����EF=FG������EF=DFDG=DFBE;
��3����ͼ3��ͬ���������ߣ��ѡ�ABD�Ƶ�A��ʱ����ת![]() ����ACG��֤����AED�ա�AEG����
����ACG��֤����AED�ա�AEG����![]() �����ɹ��ɶ�����
�����ɹ��ɶ�����![]() �ij����Ӷ��ý��ۣ�
�ij����Ӷ��ý��ۣ�
���������(1)˼·������
��ͼ1,�ѡ�ABE�Ƶ�A��ʱ����ת![]() ����ADG����ʹAB��AD�غϣ���AB=AD��
����ADG����ʹAB��AD�غϣ���AB=AD��
����ת�ã���ADG=��A=![]() ��BE=DG����DAG=��BAE��AE=AG��
��BE=DG����DAG=��BAE��AE=AG��
���FDG=��ADF+��ADG=![]() +
+![]() =
=![]() ��
��
����F. D.G���ߣ�
���ı���ABCDΪ���Σ�
���BAD=![]() ��
��
�ߡ�EAF=![]() ��
��
��![]()
��![]()
��![]()
�ڡ�AFE�͡�AFG�У�
��
���AFE�ա�AFG(SAS)��
��EF=FG��
��EF=DF+DG=DF+AE��
�ʴ�Ϊ����AFE��EF=DF+AE��
(2)������꣺

��ͼ2��EF=DFBE�������ǣ�
�ѡ�ABE�Ƶ�A��ʱ����ת![]() ����ADG����ʹAB��AD�غϣ���G��DC�ϣ�
����ADG����ʹAB��AD�غϣ���G��DC�ϣ�
����ת�ã�BE=DG����DAG=��BAE��AE=AG��
�ߡ�BAD=![]() ��
��
���BAE+��BAG=![]() ��
��
�ߡ�EAF=![]() ��
��
���FAG=![]()
![]() =
=![]() ��
��
���EAF=��FAG=![]() ��
��
�ڡ�EAF�͡�GAF�У�
��
���EAF�ա�GAF(SAS)��
��EF=FG��
��EF=DFDG=DFBE;
(3)������չ��
��ͼ3,�ѡ�ABD�Ƶ�A��ʱ����ת![]() ����ACG����ʹAB��AC�غϣ�����EG��
����ACG����ʹAB��AC�غϣ�����EG��

����ת�ã�AD=AG����BAD=��CAG��BD=CG��
�ߡ�BAC=![]() ��AB=AC��
��AB=AC��
���B=��ACB=![]() ��
��
���ACG=��B=![]() ��
��
���BCG=��ACB+��ACG=![]() +
+![]() =
=![]() ��
��
��EC=2��CG=BD=1��
�ɹ��ɶ����ã� ![]()
�ߡ�BAD=��CAG,��BAC=![]() ��
��
���DAG=![]() ��
��
�ߡ�BAD+��EAC=![]() ��
��
���CAG+��EAC=![]() =��EAG��
=��EAG��
���DAE=![]() ��
��
���DAE=��EAG=![]() ��
��
��AE=AE��
���AED�ա�AEG��
��![]()

 ȫ�ܲ����ĩС״Ԫϵ�д�
ȫ�ܲ����ĩС״Ԫϵ�д�