题目内容
【题目】有一面积为5![]() 的等腰三角形,它的一个内角是30°,则以它的腰长为边的正方形的面积为 .
的等腰三角形,它的一个内角是30°,则以它的腰长为边的正方形的面积为 .
【答案】20![]() 或20.
或20.
【解析】
试题分析:分两种情形讨论①当30度角是等腰三角形的顶角,②当30度角是底角,
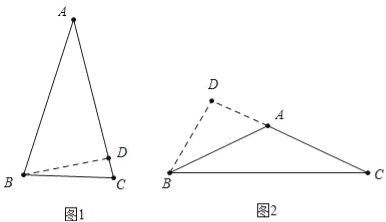
①当30度角是等腰三角形的顶角时,如图1中,
当∠A=30°,AB=AC时,设AB=AC=a,
作BD⊥AC于D,∵∠A=30°,
∴BD=![]() AB=
AB=![]() a,
a,
∴![]() a
a![]() a=5
a=5![]() ,
,
∴a2=20![]() ,
,
∴△ABC的腰长为边的正方形的面积为20![]() .
.
②当30度角是底角时,如图2中,
当∠ABC=30°,AB=AC时,作BD⊥CA交CA的延长线于D,设AB=AC=a,
∵AB=AC,
∴∠ABC=∠C=30°,
∴∠BAC=120°,∠BAD=60°,
在RT△ABD中,∵∠D=90°,∠BAD=60°,
∴BD=![]() a,
a,
∴![]() a
a![]() a=5
a=5![]() ,
,
∴a2=20,
∴△ABC的腰长为边的正方形的面积为20.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目