题目内容
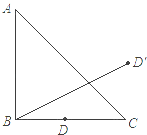
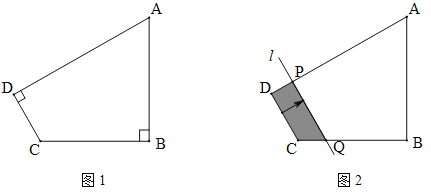
【题目】(2016四川省乐山市第23题)如图1,四边形ABCD中,∠B=∠D=90°,AB=3,BC=2,tanA=![]() .
.
(1)求CD边的长;
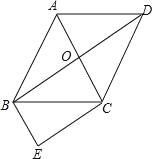
(2)如图2,将直线CD边沿箭头方向平移,交DA于点P,交CB于点Q (点Q运动到点B停止),设DP=x,四边形PQCD的面积为![]() ,求
,求![]() 与
与![]() 的函数关系式,并求出自变量
的函数关系式,并求出自变量![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() (
(![]() ).
).
【解析】
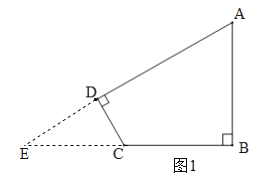
试题分析:(1)分别延长AD、BC相交于点E,在Rt△ABE中,解直角三角形可得BE,EC,AE的长,又∠E+∠A=90°,∠E+∠ECD=90°,得到∠A=∠ECD,由tanA=![]() ,得到cosA= cos∠ECD =
,得到cosA= cos∠ECD =![]() ,从而得到CD的长;
,从而得到CD的长;
(2)由(1)可知tan∠ECD=![]() ,得到ED=
,得到ED=![]() ,由PQ∥DC,可知△EDC∽△EPQ,得到PQ=
,由PQ∥DC,可知△EDC∽△EPQ,得到PQ=![]() ,由
,由![]() ,得到y=
,得到y=![]() ,而当Q点到达B点时,点P在M点处,由EC=BC,DC∥PQ,得到DM=ED=
,而当Q点到达B点时,点P在M点处,由EC=BC,DC∥PQ,得到DM=ED=![]() ,故可得自变量x的取值范围.
,故可得自变量x的取值范围.
试题解析:(1)如图1,分别延长AD、BC相交于点E,在Rt△ABE中,∵tanA=![]() ,AB=3,BC=2,∴BE=4,EC=2,AE=5,又∠E+∠A=90°,∠E+∠ECD=90°,∴∠A=∠ECD,∵tanA=
,AB=3,BC=2,∴BE=4,EC=2,AE=5,又∠E+∠A=90°,∠E+∠ECD=90°,∴∠A=∠ECD,∵tanA=![]() ,∴cosA=
,∴cosA=![]() ,∴cos∠ECD=
,∴cos∠ECD=![]() ,∴CD=
,∴CD=![]() ;
;
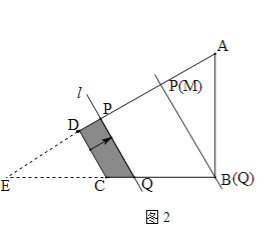
(2)由(1)可知tan∠ECD=![]() ,∴ED=
,∴ED=![]() ,如图2,由PQ∥DC,可知△EDC∽△EPQ,∴
,如图2,由PQ∥DC,可知△EDC∽△EPQ,∴![]() ,∴
,∴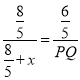 ,即PQ=
,即PQ=![]() ,∵
,∵![]() ,∴
,∴![]() ,即
,即![]() =
=![]() ,∴当Q点到达B点时,点P在M点处,由EC=BC,DC∥PQ,∴DM=ED=
,∴当Q点到达B点时,点P在M点处,由EC=BC,DC∥PQ,∴DM=ED=![]() ,∴自变量x的取值范围为:
,∴自变量x的取值范围为:![]() .
.

练习册系列答案
相关题目