题目内容
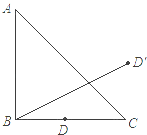
【题目】（10分）如图，在△ABC中，AB=BC，∠ABC=90°，D是BC的中点，且它关于AC的对称点是D′，BD′=
，求AC的长.
【答案】2
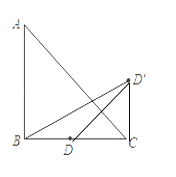
【解析】试题分析：连结CD’,DD’，D关于AC的对称点是D',可知AC垂直平分DD’, 所以CD=CD’,∠D’CD=900,设CD’=x，则BC=2x, ,在Rt△BCD’中,利用勾股定理可得BC长,进而得到AB的长.
试题解析：
连结CD’,DD’
∵AB=BC,∠ABC=900
∴∠ACB=450
∵D关于AC的对称点是D’
∴AC垂直平分DD’
∴CD=CD’,∠D’CD=900
又∵D是BC的中点，
∴BC=2CD’
设CD’= 
，则BC=2
∴在Rt△BCD’中
由勾股定理得：CD’2+BC2=BD’2,
∴AB=BC=2
∴AC=2
练习册系列答案
名校通行证有效作业系列答案
相关题目
