题目内容
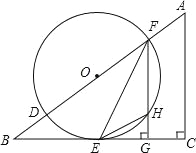
【题目】(2016广东省茂名市第24题)如图,在△ABC中,∠C=90°,D、F是AB边上的两点,以DF为直径的⊙O与BC相交于点E,连接EF,过F作FG⊥BC于点G,其中∠OFE=![]() ∠A.
∠A.
(1)求证:BC是⊙O的切线;
(2)若sinB=![]() ,⊙O的半径为r,求△EHG的面积(用含r的代数式表示).
,⊙O的半径为r,求△EHG的面积(用含r的代数式表示).
【答案】(1)、证明过程见解析;(2)、![]()
【解析】
试题分析:(1)、首先连接OE,由在△ABC中,∠C=90°,FG⊥BC,可得FG∥AC,又由∠OFE=![]() ∠A,易得EF平分∠BFG,继而证得OE∥FG,证得OE⊥BC,则可得BC是⊙O的切线;(2)、由在△OBE中,sinB=
∠A,易得EF平分∠BFG,继而证得OE∥FG,证得OE⊥BC,则可得BC是⊙O的切线;(2)、由在△OBE中,sinB=![]() ,⊙O的半径为r,可求得OB,BE的长,然后由在△BFG中,求得BG,FG的长,则可求得EG的长,易证得△EGH∽△FGE,然后由相似三角形面积比等于相似比的平方,求得答案.
,⊙O的半径为r,可求得OB,BE的长,然后由在△BFG中,求得BG,FG的长,则可求得EG的长,易证得△EGH∽△FGE,然后由相似三角形面积比等于相似比的平方,求得答案.
试题解析:(1)、连接OE, ∵在△ABC中,∠C=90°,FG⊥BC, ∴∠BGF=∠C=90°, ∴FG∥AC,
∴∠OFG=∠A, ∴∠OFE=![]() ∠OFG, ∴∠OFE=∠EFG, ∵OE=OF, ∴∠OFE=∠OEF, ∴∠OEF=∠EFG,
∠OFG, ∴∠OFE=∠EFG, ∵OE=OF, ∴∠OFE=∠OEF, ∴∠OEF=∠EFG,
∴OE∥FG, ∴OE⊥BC, ∴BC是⊙O的切线;
(2)、∵在Rt△OBE中,sinB=![]() ,⊙O的半径为r, ∴OB=
,⊙O的半径为r, ∴OB=![]() r,BE=
r,BE=![]() r, ∴BF=OB+OF=
r, ∴BF=OB+OF=![]() r,
r,
∴FG=BFsinB=![]() r, ∴BG=
r, ∴BG=![]() =
=![]() r, ∴EG=BG﹣BE=
r, ∴EG=BG﹣BE=![]() r,
r,
∴S△FGE=![]() EGFG=
EGFG=![]() r2,EG:FG=1:2, ∵BC是切线, ∴∠GEH=∠EFG, ∵∠EGH=∠FGE,
r2,EG:FG=1:2, ∵BC是切线, ∴∠GEH=∠EFG, ∵∠EGH=∠FGE,
∴△EGH∽△FGE, ∴![]() =(
=(![]() )=
)=![]() , ∴S△EHG=
, ∴S△EHG=![]() S△FGE=
S△FGE=![]() r2.
r2.


练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目