题目内容
【题目】将7张相同的小长方形纸片(如图1所示)按图2所示的方式不重叠的放在长方形ABCD内,未被覆盖的部分恰好被分割为两个长方形,面积分别为S1和S2.已知小长方形纸片的长为a,宽为b,且a>b.
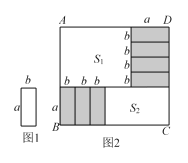
(1)当a=9,b=3,AD=30时,长方形ABCD的面积是 ,S2-S1的值为 .
(2)当AD=40时,请用含a、b的式子表示 S2-S1的值;
(3)若AB长度为定值,AD变长,将这7张小长方形纸片还按照同样的方式放在新的长方形ABCD内,而S2-S1 的值总保持不变,则a、b 满足的关系是 .
【答案】(1)630;-63;(2)40a-160b+ab;(3)a=4b
【解析】试题分析:(1)根据长方形的面积公式,直接计算即可;求出S1和S2的面积,相减即可;
(2)用含a、b的式子表示出S1和S2的面积,即可求得结论;
(3)用含a、b、AD的式子表示出S2-S1,根据S2-S1的值总保持不变,即与AD的值无关,整理后,让AD的系数为0即可.
试题解析:(1)长方形ABCD的面积为30×(4×3+9)=630;S2-S1=(30-9)×9-(30-9)×4×3=-63;
(2)S2-S1=a(30-3b)-4b(30-a)=40a-160b+ab;
(3)∵S2-S1= a(AD-3b)-4b(AD-a),
整理,得:S2-S1=(a -4b)AD+ab,
∵若AB长度不变,AD变长,而S2-S1的值总保持不变,
∴a - 4b=0,
解得:a=4b.
即a,b满足的关系是a=4b.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目