题目内容
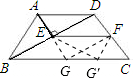
如图,梯形ABCD中,AD∥BC,AB=AD=DC=2,∠C=60°,AE⊥BD于点E,F是CD的中点,连接EF.
(1)求证:四边形AEFD是平行四边形;
(2)若点G是BC边上的一个动点,当点G在什么位置时,四边形DEFG是矩形?并求出这个矩形的周长;
(3)在BC上能否找到另外一点G′,使四边形DEG′F的周长与(2)中矩形DEFG的周长相等,请简述你的理由.

(1)求证:四边形AEFD是平行四边形;
(2)若点G是BC边上的一个动点,当点G在什么位置时,四边形DEFG是矩形?并求出这个矩形的周长;
(3)在BC上能否找到另外一点G′,使四边形DEG′F的周长与(2)中矩形DEFG的周长相等,请简述你的理由.

(1)证明:∵梯形ABCD中,AD∥BC,AB=AD=DC=2,
∴四边形ABCD为等腰梯形,∠C=60°,
∴∠BAD=∠ADC=120°,
又∵△ABD为等腰三角形,AE⊥BD,
∴∠EAD=
∠BAD=60°,BE=DE,
在Rt△ADE中,∠ADE=90°-∠EAD=30°,
∴∠BDC=∠ADC-∠ADE=90°,
∴AE∥DF,
∵E、F两点为BD、CD边的中点,
∴EF∥BC∥AD,
∴四边形AEFD是平行四边形;
(2)延长AE交BC于G,连接FG,
∵BE=ED,AE∥CD,∴AD=BG=GC,
∴G点为BC的中点,
∴FG∥DE,
而∠EDF=90°,
∴四边形DEGF是矩形,
在Rt△DEF中,DE=
,DF=1,
∴矩形的周长=2+2
;
(3)可以.
当CG′=CF=1时,△G′EF与△DEF关于直线EF轴对称,
DF=FG′,DE=EG′,
则四边形DEG′F的周长=2+2
;
周长不变.
∴四边形ABCD为等腰梯形,∠C=60°,
∴∠BAD=∠ADC=120°,
又∵△ABD为等腰三角形,AE⊥BD,
∴∠EAD=
| 1 |
| 2 |
在Rt△ADE中,∠ADE=90°-∠EAD=30°,
∴∠BDC=∠ADC-∠ADE=90°,
∴AE∥DF,
∵E、F两点为BD、CD边的中点,
∴EF∥BC∥AD,
∴四边形AEFD是平行四边形;
(2)延长AE交BC于G,连接FG,
∵BE=ED,AE∥CD,∴AD=BG=GC,
∴G点为BC的中点,
∴FG∥DE,
而∠EDF=90°,
∴四边形DEGF是矩形,
在Rt△DEF中,DE=
| 3 |
∴矩形的周长=2+2
| 3 |
(3)可以.
当CG′=CF=1时,△G′EF与△DEF关于直线EF轴对称,
DF=FG′,DE=EG′,
则四边形DEG′F的周长=2+2
| 3 |
周长不变.


练习册系列答案
相关题目




 D上,将△AEF沿EF翻折,点A的落点记为P.
D上,将△AEF沿EF翻折,点A的落点记为P.
 之停止运动,设运动的时间为t秒.
之停止运动,设运动的时间为t秒.