��Ŀ����
����Ŀ����12�֣���ͼ����ֱ������ϵ�У�Rt��OAB��ֱ�Ƕ���A��x���ϣ�OA=4��AB=3������M�ӵ�A��������ÿ��1����λ���ȵ��ٶȣ���AO���յ�O�ƶ���ͬʱ��N�ӵ�O��������ÿ��1��25����λ���ȵ��ٶȣ���OB���յ�B�ƶ��������������˶���x�루0��x��4��ʱ������������⣺
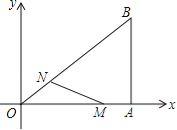
��1�����N�����꣨�ú�x�Ĵ���ʽ��ʾ����
��2������OMN�������S����S��x֮��ĺ�������ʽ����xΪ��ֵʱ��S�����ֵ�����ֵ�Ƕ��٣�
��3�������������˶������У��Ƿ����ijһʱ�̣�ʹ��OMN��ֱ�������Σ������ڣ����x��ֵ���������ڣ���˵�����ɣ�
���𰸡���1����x�� ![]() ����
����
��2����x=2ʱ��S�����ֵ�����ֵ��![]() ��
��
��3��x��ֵ��2���![]() �룮
�룮
�����������⣨1���ɹ��ɶ������OB����NP��OA��P����NP��AB���ó���OPN�ס�OAB���ó�����ʽ![]() �����OP��PN�����ɵó���N�����ꣻ
�����OP��PN�����ɵó���N�����ꣻ
��2���������ε������ʽ�ó�S��x�Ķ��κ��������ɵó�S�����ֵ��
��3�������������������OMN=90������MN��AB����ƽ���ߵó���OMN�ס�OAB���ó�����ʽ���������x��ֵ��
������ONM=90��������ONM=��OAB��֤����OMN�ס�OBA���ó�����ʽ�����x��ֵ���ɣ�
����������⣺��1����������ã�MA=x��ON=1��25x��
��Rt��OAB�У��ɹ��ɶ����ã�OB=![]() =5��
=5��
��NP��OA��P����ͼ1��ʾ��
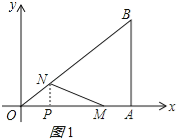
��NP��AB��
���OPN�ס�OAB��
��![]() ��
��
��![]() ��
��
��ã�OP=x��PN= ![]() ��
��
����N�������ǣ�x�� ![]() ����
����
��2������OMN�У�OM=4��x��OM���ϵĸ�PN= ![]() ��
��
��S=![]() OMPN=
OMPN=![]() ��4��x��
��4��x�� ![]() =��
=��![]()
![]() +
+![]() x��
x��
��S��x֮��ĺ�������ʽΪS=��![]()
![]() +
+![]() x��0��x��4����
x��0��x��4����
�䷽�ã�S=��![]()
![]() +
+![]() ��
��
����![]() ��0��
��0��
��S�����ֵ��
��x=2ʱ��S�����ֵ�����ֵ��![]() ��
��
��3������ijһʱ�̣�ʹ��OMN��ֱ�������Σ��������£�
�����������������OMN=90������ͼ2��ʾ��
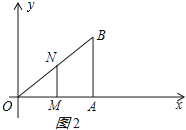
��MN��AB��
��ʱOM=4��x��ON=1��25x��
��MN��AB��
���OMN�ס�OAB��
��![]() ��
��
��![]() ��
��
��ã�x=2��
������ONM=90������ͼ3��ʾ��
����ONM=��OAB��
��ʱOM=4��x��ON=1��25x��
�ߡ�ONM=��OAB����MON=��BOA��
���OMN�ס�OBA��
��![]() ��
��
��![]() ��
��
��ã�x=![]() ��
��
����������x��ֵ��2���![]() �룮
�룮