题目内容
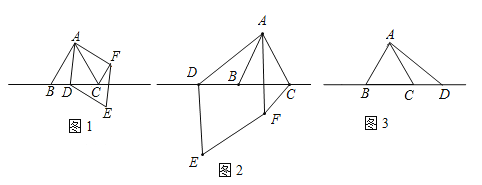
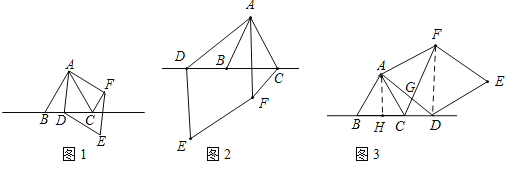
【题目】△ABC中,∠BAC=60°,AB=AC,点D为直线BC上一动点(点D不与B,C重合),以AD为边在AD右侧作菱形ADEF,使∠DAF=60°,连接CF.
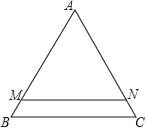
(1)观察猜想:如图1,当点D在线段BC上时,①AB与CF的位置关系为: ;
②BC,CD,CF之间的数量关系为: .
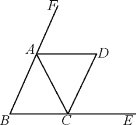
(2)数学思考:如图2,当点D在线段CB的延长线上时,结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.
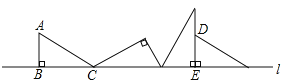
(3)拓展延伸:如图3,当点D在线段BC的延长线上时,设AD与CF相交于点G,若已知AB=4,CD=![]() AB,求AG的长.
AB,求AG的长.
【答案】(1) ①AB∥CF ; ②BC=CD+CF;(2)见解析;(3)![]() .
.
【解析】(1)①根据菱形的性质以及等边三角形的性质,推出△DAB≌△FAC,根据全等三角形的性质即可得到结论;②根据全等三角形的性质得到CF=BD,再根据BD+CD=BC,即可得出CF+CD=BC;
(2)依据△ABD≌△ACF,即可得到∠ACF+∠BAC=180°,进而得到AB∥CF;依据△ABD≌△ACF可得BD=CF,依据CD﹣BD=BC,即可得出CD﹣CF=BC;
(3)判定△ABD≌△ACF,即可得到CF=BD=BC+CD=6,∠ACG=∠ABC=60°=∠ADF,再根据△AGC∽△FGD,即可得到![]() =
=![]() =
=![]() ,进而得出AG的长.
,进而得出AG的长.
(1)①∵∠BAC=60°,AB=AC,∴△ABC是等边三角形,∴∠BAC=60°=∠DAF,∴∠BAD=∠CAF.
又∵菱形ADEF中,AD=AF,∴△ABD≌△ACF,∴∠ACF=∠ABD=60°.
又∵∠ACB=60°,∴∠ABC+∠BCF=180°,∴AB∥CF;
②∵△ABD≌△ACF,∴BD=CF.
又∵BD+CD=BC,∴CF+CD=BC.
故答案为:AB∥CF;CF+CD=BC;
(2)结论①成立,而结论②不成立.证明如下:
如图2.∵∠BAC=60°,AB=AC,∴△ABC是等边三角形,∴∠BAC=60°=∠DAF,∠ABD=120°,∴∠BAD=∠CAF.
又∵菱形ADEF中,AD=AF,∴△ABD≌△ACF,∴∠ACF=∠ABD=120°.
又∵∠CAB=60°,∴∠ACF+∠BAC=180°,∴AB∥CF;
∵△ABD≌△ACF, ∴BD=CF.
又∵CD﹣BD=BC,∴CD﹣CF=BC;
(3)如图3,连接DF,过A作AH⊥BD于H,则AH=2![]() ,DH=2+2=4,∴Rt△ADH中,AD=2
,DH=2+2=4,∴Rt△ADH中,AD=2![]() .
.
∵AF=AD,∠DAF=60°,∴△ADF是等边三角形.
又∵∠BAC=60°,AB=AC,∠BAD=∠CAF,∴△ABD≌△ACF,∴CF=BD=BC+CD=6,∠ACG=∠ABC=60°=∠ADF.
又∵∠AGC=∠FGD,∴△AGC∽△FGD,∴![]() =
=![]() =
=![]() =
=![]() ,∴可设AG=4x,则FG=2
,∴可设AG=4x,则FG=2![]() x,CG=6﹣2
x,CG=6﹣2![]() x,DG=2
x,DG=2![]() ﹣4x,∴
﹣4x,∴![]() =
=![]() ,解得:x=
,解得:x=![]() ,∴AG=
,∴AG=![]() .
.

【题目】小东根据学习函数的经验,对函数![]() 的图象与性质进行了探究.下面是小东的探究过程,请补充完整,并解决相关问题:
的图象与性质进行了探究.下面是小东的探究过程,请补充完整,并解决相关问题:
(1)函数![]() 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;
(2)下表是y与x的几组对应值.
x | … |
|
|
| 0 |
| 1 |
| 2 |
| 3 | 4 | … |
y | … |
|
|
| 2 |
| 4 |
| 2 |
|
| m | … |
表中m的值为________________;
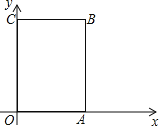
(3)如图,在平面直角坐标系中,描出了以上表中各对对应值为坐标的点. 根据描出的点,画出函数![]() 的大致图象;
的大致图象;
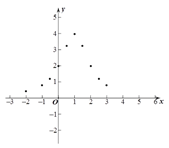
(4)结合函数图象,请写出函数![]() 的一条性质:______________________.
的一条性质:______________________.
(5)解决问题:如果函数![]() 与直线y=a的交点有2个,那么a的取值范围是______________ .
与直线y=a的交点有2个,那么a的取值范围是______________ .