题目内容
【题目】探究
(1)已知如图1，若AB∥CD，P为平行线内的一点请你判断∠B+∠P+∠D= 度，并说明理由.
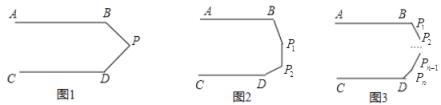
(2)如图2，若AB∥CD ，P1、P2为平行线内的两个点，请求出∠B+∠P1+∠P2+∠D= 度(不需要说明理由)
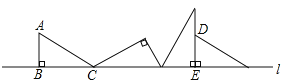
(3)如图3，如此类推若AB∥CD，P1、、P2、P3、P4、……Pn为平行线内的n个点，请求出∠B+∠P1+∠P2+∠P3+……．+∠Pn-1+∠Pn+∠D= 度(不需要说明理由)
【答案】（1）360°；（2）540°；（3）
【解析】
（1）过点P作AB的平行线PE，利用平行线的性质，即可得到∠B+∠BPD+∠D=180°×2=360°；
（2）过P1作P1F∥AB，过P2作P2G∥CD，则利用平行线的性质，即可得到∠B+∠BP1P2+∠P1P2D+∠D的度数；
（3）利用（1）（2）中的结论，找出规律，即可得到∠A+∠C1+∠C2+……+∠Cn+1+∠D的度数．
解：（1）如图，过点P作AB的平行线PE，
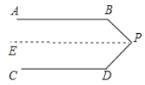
∵AB∥CD，AB∥PE，
∴∠B+∠BPE=180°，∠D+∠DPE=180°，
∵∠BPD=∠BPE+∠DPE，
∴∠B+∠BPD+∠D=180°×2=360°；
故答案为：360°.
（2）如图，过P1作C1F∥AB，过P2作P2G∥DE，
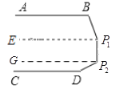
∵AB∥CD，P1F∥AB，过P2作P2G∥CD，
∴∠B+∠BP1F=180°，∠FP1P2+∠P1P2G=180°，∠GP2D+∠D=180°，
∵∠BP1P2=∠BP1F+∠FP1P2，∠P1P2D=∠P1P2G+∠GP2D，
∴∠B+∠BP1P2+∠P1P2D+∠D=180°×3=540°；
故答案为：540°.
（3）由（1）（2）可知，
当B、D两点之间有1个点时，∠B+∠BPD+∠D=180°×2=360°；
当B、D两点之间有2个点时，∠B+∠BP1P2+∠P1P2D+∠D=180°×3=540°；
……
当B、D两点之间有n个点时，有
∠A+∠C1+∠C2+……+∠Cn+1+∠D=180°（n+1）；
故答案为：.
