题目内容
【题目】[问题]小明在学习时遇到这样一个问题:求不等式x3+3x2﹣x﹣3>0的解集.
他经历了如下思考过程:
[回顾]
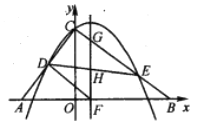
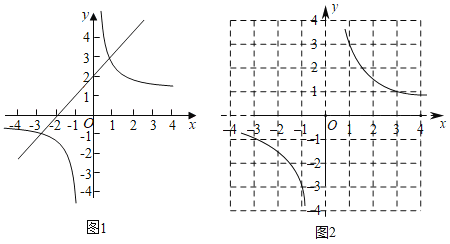
(1)如图1,在平面直角坐标系xOy中,直线y1=ax+b与双曲线y2=![]() 交于A (1,3)和B(﹣3,﹣1),则不等式ax+b>
交于A (1,3)和B(﹣3,﹣1),则不等式ax+b>![]() 的解集是 .
的解集是 .
[探究]将不等式x3+3x2﹣x﹣3>0按条件进行转化:
当x=0时,原不等式不成立;
当x>0时,不等式两边同除以x并移项转化为x2+3x﹣1>![]() ;
;
当x<0时,不等式两边同除以x并移项转化为x2+3x﹣1<![]() .
.
(2)构造函数,画出图象:
设y3=x2+3x﹣1,y4=![]() ,在同一坐标系中分别画出这两个函数的图象;
,在同一坐标系中分别画出这两个函数的图象;
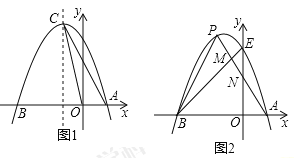
双曲线y4=![]() 如图2所示,请在此坐标系中画出抛物线y=x2+3x﹣1.(不用列表)
如图2所示,请在此坐标系中画出抛物线y=x2+3x﹣1.(不用列表)
(3)确定两个函数图象公共点的横坐标:
观察所画两个函数的图象,猜想并通过代入函数解析式验证可知:满足y3=y4的所有x的值为 .
[解决]
(4)借助图象,写出解集:
结合“探究”中的讨论,观察两个函数的图象可知:不等式x3+3x2﹣x﹣3>0的解集为 .
【答案】(1)x>1或﹣3<x<0;(2)详见解析;(3)﹣3或﹣1或1;(4)x>1或x<﹣3或﹣1<x<0.
【解析】
(1)根据一次函数与反比例函数图像位置关系直接观察出不等式解集.
(2)找出该函数上的关键点,在图表中描点连线即可.
(3)由图像观察即可得出交点的横坐标,即为原方程的解.
(4)根据(3)小问的方法,将原式转化为x2+3x﹣1>![]() ,作图找交点即可(注意讨论x与0的大小关系).
,作图找交点即可(注意讨论x与0的大小关系).
解:(1)如图1中,观察图形可知:不等式ax+b>![]() 的解集为x>1或﹣3<x<0.
的解集为x>1或﹣3<x<0.
故答案为:x>1或﹣3<x<0.
(2)函数y3=x2+3x﹣1的图形如图所示:
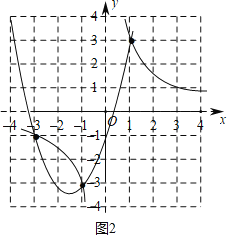
(3)观察图象可知,两个函数图象的公共点的横坐标为﹣3,﹣1,1.
经过检验可知:点(﹣3,﹣1),点(﹣1,﹣3),点(1,3)是两个函数的交点坐标,
满足y3=y4的所有x的值为﹣3或﹣1或1.
故答案为﹣3或﹣1或1.
(4)观察图象,当x>0时,不等式两边同除以x并移项转化为x2+3x﹣1>![]() 的解集为x>1,
的解集为x>1,
当x<0时,不等式两边同除以x并移项转化为x2+3x﹣1<![]() 的解集为x<﹣3或﹣1<x<0,
的解集为x<﹣3或﹣1<x<0,
∴不等式x3+3x2﹣x﹣3>0的解集为x>1或x<﹣3或﹣1<x<0.
故答案为x>1或x<﹣3或﹣1<x<0.

【题目】某工厂生产部门为了解本部门工人的生产能力情况,进行了抽样调查.该部门随机抽取了30名工人某天每人加工零件的个数,数据如下:
20 | 21 | 19 | 16 | 27 | 18 | 31 | 29 | 21 | 22 |
25 | 20 | 19 | 22 | 35 | 33 | 19 | 17 | 18 | 29 |
18 | 35 | 22 | 15 | 18 | 18 | 31 | 31 | 19 | 22 |
整理上面数据,得到条形统计图:
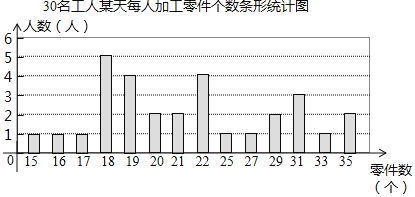
样本数据的平均数、众数、中位数如下表所示:
统计量 | 平均数 | 众数 | 中位数 |
数值 | 23 | m | 21 |
根据以上信息,解答下列问题:
(1)上表中众数m的值为 ;
(2)为调动工人的积极性,该部门根据工人每天加工零件的个数制定了奖励标准,凡达到或超过这个标准的工人将获得奖励.如果想让一半左右的工人能获奖,应根据 来确定奖励标准比较合适.(填“平均数”、“众数”或“中位数”)
(3)该部门规定:每天加工零件的个数达到或超过25个的工人为生产能手.若该部门有300名工人,试估计该部门生产能手的人数.