Question

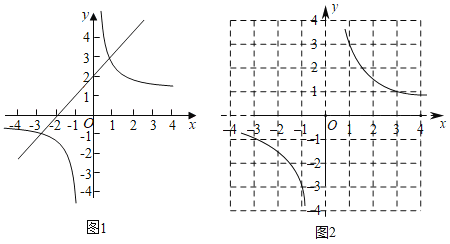
【题目】如图1，已知抛物线过点．

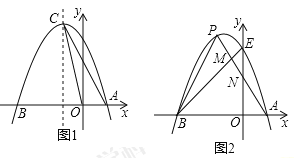
（1）求抛物线的解析式及其顶点C的坐标；

（2）设点D是x轴上一点，当时，求点D的坐标；

（3）如图2．抛物线与y轴交于点E，点P是该抛物线上位于第二象限的点，线段PA交BE于点M，交y轴于点N，和的面积分别为，求的最大值．

Answer 1

【答案】（1），顶点C的坐标为-（-1,4）；（2）；（3）的最大值为.

【解析】

（1）利用待定系数法，将A，B的坐标代入即可求得二次函数的解析式；

（2）设抛物线对称轴与x轴交于点H，在中，可求得，推出，可证，利用相似三角形的性质可求出AD的长度，进一步可求出点D的坐标，由对称性可直接求出另一种情况；

（3）设代入，求出直线PA的解析式，求出点N的坐标，由，可推出，再用含a的代数式表示出来，最终可用函数的思想来求出其最大值．

解：（1）由题意把点代入，

得，，

解得，

∴此抛物线解析式为：，顶点C的坐标为

（2）∵抛物线顶点，

∴抛物线对称轴为直线，

设抛物线对称轴与x轴交于点H，

则，

在中，，

，

∴当时，

如图1，当点D在对称轴左侧时，

，

，

，

，

，

当点D在对称轴右侧时，点D关于直线的对称点D'的坐标为，

∴点D的坐标为或；

（3）设，

将代入，

得，，

解得，，

当时，，

如图2，

，

由二次函数的性质知，当时，有最大值，

和的面积分别为m、n，

的最大值为．