Question

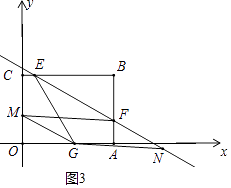
【题目】如图，四边形OABC为矩形，A点在x轴上，C点在y轴上，矩形一角经过翻折后，顶点B落在OA边的点G处，折痕为EF，F点的坐标是（4，1），∠FGA=30°．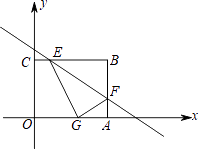

（1）求B点坐标．
（2）求直线EF解析式．
（3）若点M在y轴上，直线EF上是否存在点N，使以M、N、F、G为顶点的四边形是平行四边形？若存在，求N点的坐标；若不存在，请说明理由．

Answer 1

【答案】
（1）解：∵F点的坐标是（4，1），

∴FA=1，OA=4，

∵∠FGA=30°，

∴GA= ，FG=2，

由折叠的性质知BF=FG=2，

∴AB=3，

∵四边形OABC为矩形，

∴CB=OA=4，

∴B点坐标为（4，3）；

（2）解：∠AFG=90°﹣30°=60°，由折叠的性质知∠EFB=∠EFG= （180°﹣60°）=60°，

∴BE= BF=2 ，

∴CE=4﹣2 ，

∴E（4﹣2 ，4），

设直线EF的解析式是y=kx+b，

∴ ，

解得 ，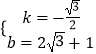

∴直线EF的解析式是y=﹣ x+2 +1

（3）解：①如图1中，当四边形MNGF是平行四边形时，易知点N的横坐标为﹣ ，

∵点N在直线EF上，

∴N（﹣ ，2 + ）．

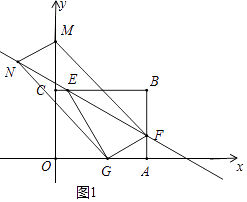
②如图2中，当四边形MNFG是平行四边形时，易知点N的横坐标为 ，

∵点N在直线EF上，

∴N（ ，2 ﹣ ）．

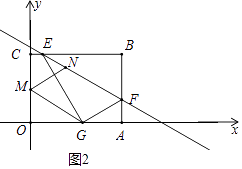
③如图3中，当四边形MFNG是平行四边形时，易知点M坐标为（0， ）

∵FG与MN相互垂直平分，

∴N（8﹣ ，2﹣ ）．

【解析】（1）利用翻折不变性即可解决问题；（2）求出E、F两点坐标，利用待定系数法即可解决问题；（3）分三种情形①如图1中，当四边形MNGF是平行四边形时，易知点N的横坐标为﹣ ，由此即可解决问题；②如图2中，当四边形MNFG是平行四边形时，易知点N的横坐标为 ，由此即可解决问题；③如图3中，当四边形MFNG是平行四边形时，易知点M坐标为（0， ），根据FG与MN相互垂直平分，利用中点坐标公式，计算即可；
【考点精析】通过灵活运用确定一次函数的表达式和勾股定理的概念，掌握确定一个一次函数，需要确定一次函数定义式y=kx+b（k不等于0）中的常数k和b．解这类问题的一般方法是待定系数法；直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2即可以解答此题．