��Ŀ����
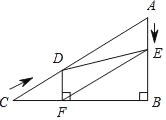
����Ŀ����ͼ����Rt��ABC�У���B��90�㣬AC��60cm����A��60�㣬��D�ӵ�C������CA������4cm/s���ٶ����A�����˶���ͬʱ��E�ӵ�A������AB������2cm/s���ٶ����B�����˶���������һ���㵽���յ�ʱ����һ����Ҳ��ֹ֮ͣ�˶������D��E�˶���ʱ����ts������D��DF��BC�ڵ�F������DE��EF��
��1����֤��AE��DF��
��2���ı���AEFD�ܹ���Ϊ����������ܣ������Ӧ��tֵ��������ܣ���˵�����ɣ�
��3����tΪ��ֵʱ����DEFΪֱ�������Σ���˵�����ɣ�
���𰸡���1�������������2����t��10ʱ��AEFD�����Σ���3����t��![]() ʱ����DEF��ֱ�������Σ���EDF��90�㣩����t��12ʱ����DEF��ֱ�������Σ���DEF��90�㣩��
ʱ����DEF��ֱ�������Σ���EDF��90�㣩����t��12ʱ����DEF��ֱ�������Σ���DEF��90�㣩��
��������
��1����Rt��ABC�У�������֪���������C��30�����������֪CD��4tcm��AE��2tcm����ֱ����CDF�У�����30���ֱ�������ε����ʿɵ�DF��![]() CD��2tcm���ɴ˼���֤��DF��AE����2����DF��AB��DF��AE������һ��Ա�ƽ������ȵ��ı�����ƽ���ı��οɵ��ı���AEFD��ƽ���ı��Σ���AD��AEʱ���ı���AEFD�����Σ����ɵ�60��4t��2t�����t��10������t��10ʱ��AEFD�����Σ���2���ܣ�����EDF��90������DEF��90�����������t��ֵ���ɣ�
CD��2tcm���ɴ˼���֤��DF��AE����2����DF��AB��DF��AE������һ��Ա�ƽ������ȵ��ı�����ƽ���ı��οɵ��ı���AEFD��ƽ���ı��Σ���AD��AEʱ���ı���AEFD�����Σ����ɵ�60��4t��2t�����t��10������t��10ʱ��AEFD�����Σ���2���ܣ�����EDF��90������DEF��90�����������t��ֵ���ɣ�
��1��֤��������Rt��ABC�У���B��90�㣬AC��60cm����A��60�㣬
���C��90�㩁��A��30�㣮
�������֪��CD��4tcm��AE��2tcm��
�֡���ֱ�ǡ�CDF�У���C��30�㣬
��DF��![]() CD��2tcm��
CD��2tcm��
��DF��AE��
��2����DF��AB��DF��AE��
���ı���AEFD��ƽ���ı��Σ�
��AD��AEʱ���ı���AEFD�����Σ�
��60��4t��2t��
��ã�t��10��
����t��10ʱ��AEFD�����Σ�

��3����t��![]() ʱ��DEF��ֱ�������Σ���EDF��90�㣩����t��12ʱ����DEF��ֱ�������Σ���DEF��90�㣩��
ʱ��DEF��ֱ�������Σ���EDF��90�㣩����t��12ʱ����DEF��ֱ�������Σ���DEF��90�㣩��
�������£�
����EDF��90��ʱ��DE��BC��
���ADE����C��30��
��AD��2AE
��CD��4tcm��
��DF��AE��2tcm��
��AD��2AE��4tcm��
��4t+4t��60��
��t��![]() ʱ����EDF��90�㣮
ʱ����EDF��90�㣮
����DEF��90��ʱ��DE��EF��
���ı���AEFD��ƽ���ı��Σ�
��AD��EF��
��DE��AD��
���ADE��ֱ�������Σ���ADE��90�㣬
�ߡ�A��60�㣬
���DEA��30�㣬
��AD��![]() AE��
AE��
AD��AC��CD��60��4t��cm����AE��DF��![]() CD��
CD��
��60��4t��t��
���t��12��
������������t��![]() ʱ��DEF��ֱ�������Σ���EDF��90�㣩����t��12ʱ����DEF��ֱ�������Σ���DEF��90�㣩��
ʱ��DEF��ֱ�������Σ���EDF��90�㣩����t��12ʱ����DEF��ֱ�������Σ���DEF��90�㣩��