题目内容
【题目】已知正比例函数![]() 与反比例函数
与反比例函数![]() .
.
(1)证明:直线与双曲线没有交点;
(2)若将直线![]() 向上平移4个单位后与双曲线恰好有且只有一个交点,求反比例函数的表达式和平移后的直线表达式;
向上平移4个单位后与双曲线恰好有且只有一个交点,求反比例函数的表达式和平移后的直线表达式;
(3)将(2)小题平移后的直线代表的函数记为![]() ,根据图象直接写出:对于负实数
,根据图象直接写出:对于负实数![]() ,当
,当![]() 取何值时
取何值时![]()
【答案】(1)方程组无解即没有公共解,也就是两函数图象没有交点(交点即公共点);(2)当![]() 时,
时,![]()
![]() 当
当![]() 时,
时,![]()
![]() ;(3)当
;(3)当![]() 或
或![]() 时满足
时满足![]() .
.
【解析】
(1)将![]() 和
和![]() 这两函数看成两个不定方程,联立方程组,整理后得方程
这两函数看成两个不定方程,联立方程组,整理后得方程![]() ,再利用根的判别式得出这个方程无解,所以两函数图象没有交点;
,再利用根的判别式得出这个方程无解,所以两函数图象没有交点;
(2)向上平移4个单位后![]() ,联立方程组,整理后得方程
,联立方程组,整理后得方程![]() ,因为直线
,因为直线![]() 与双曲线
与双曲线![]() 有且只有一个交点,所以方程
有且只有一个交点,所以方程![]() 有且只有一个解,利用根的判别式得出K的值,从而得到函数表达式;
有且只有一个解,利用根的判别式得出K的值,从而得到函数表达式;
(3)取![]() 时,作出函数图象,观察图象可得到结论.
时,作出函数图象,观察图象可得到结论.
(1)证明:将![]() 和
和![]() 这两函数看成两个不定方程,联立方程组得:
这两函数看成两个不定方程,联立方程组得:

![]()
两边同时乘![]() 得
得![]() ,
,
整理后得![]()
利用![]() 计算验证得:
计算验证得:
![]()
∵![]() 所以
所以![]()
方程组无解即没有公共解,也就是两函数图象没有交点(交点即公共点)
(2)向上平移4个单位后![]() ,这时刚好与双曲线有且只有一个交点.
,这时刚好与双曲线有且只有一个交点.
联立方程组得:

![]()
两边同时乘![]() 得
得![]() ,整理后得
,整理后得![]()
因为直线![]() 与双曲线
与双曲线![]() 有且只有一个交点,
有且只有一个交点,
∴方程![]() 有且只有一个解,即:
有且只有一个解,即:![]() ,
,
将方程对应的![]() 值代入判别式得:
值代入判别式得:![]()
解得![]()
综上所述:当![]() 时,
时,![]() ,
, ![]()
当![]() 时,
时,![]() ,
, ![]()
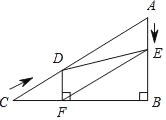
(3)题目要求负实数![]() 的值,所以我们取
的值,所以我们取![]() 时的函数图象情况.图象大致如下图所示:
时的函数图象情况.图象大致如下图所示:

计算可得交点坐标![]() ,
,
要使![]() ,即函数
,即函数![]() 的图象在函数
的图象在函数![]() 图象的上方即可,
图象的上方即可,
由图可知,当![]() 或
或![]() 时函数
时函数![]() 的图象在函数
的图象在函数![]() ,
,
图象的上方,即当![]() 或
或![]() 时满足
时满足![]()

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目