题目内容
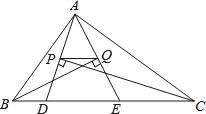
【题目】如图,已知:在ABCD中,E、F分别是AD、BC边的中点,G、H是对角线BD上的两点,且BG=DH,则下列结论中不正确的是( )
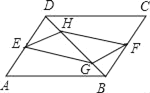
A. GF⊥FHB. GF=EH
C. EF与AC互相平分D. EG=FH
【答案】A
【解析】
连接EF交BD于O,易证四边形EGFH是平行四边形,然后证明是否得出选项.
连接EF交BD于点O,
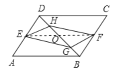
在平行四边形ABCD中的AD=BC,∠EDH=∠FBG,
∵E、F分别是AD、BC边的中点,
∴DE∥BF,DE=BF=![]() BC,
BC,
∴四边形AEFB是平行四边形,有EF∥AB,
∵点E是AD的中点,
∴点O是BD的中点,根据平行四边形中对角线互相平分,故点O也是AC的中点,也是EF的中点,故C正确,
又∵BG=DH,∴△DEH≌△BFG,
∴GF=EH,故B正确,
∠DHE=∠BGF,∴∠GHE=∠HGF,
∴△EHG≌△FGH,
∴EG=HF,故D正确,
∴GF∥EH,即四边形EHFG是平行四边形,而不是矩形,故∠GFH不是90度,
∴A不正确。
故选A.

练习册系列答案
相关题目