��Ŀ����
����Ŀ�����壺����ABC�У�����һ���ڽ�����һ���ڽǵ�һ�룬�����ABCΪ������������������ݴ˶��壬���������⣺
��1������ABCΪ��������Σ��ҡ�A��90��������ABC�����������ǵĶ���Ϊ�� ����
��2������ABC�ǰ�������Σ��ҡ�C��40�������B�� ����
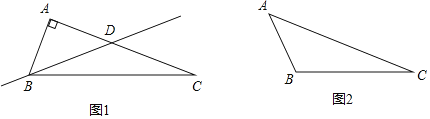
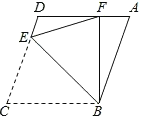
��3����ͼ�����ı���ABCD�У�AB��CD��AD��BC����C��72������E�ڱ�CD�ϣ���BEΪ�ۺۣ�����BCE���Ϸ��ۣ���Cǡ������AD���ϵĵ�F����BF��AD������EDF�ǰ�������������ǣ���˵�����ɣ�
���𰸡���1��45����45����30����60������2��20����80����60����120����![]() ����
����![]() ������3����EDF�ǰ�������Σ����ɼ�����
������3����EDF�ǰ�������Σ����ɼ�����
��������
��1��������������н�𣬢�����һ����ǵ��ڡ�A��90����һ�룬��������A������������У���һ��������һ����һ�룬���������ε��ڽǺ�Ϊ180�������н��
��2������������������۽�𣬰����е�һ���ڽǵ�����һ���ڽǵ�һ�����������п��ǣ��ֱ������Ӧ�ĽǵĶ�����
��3����������ֱ����������DEF�ĸ����ڽǵĶ�������������������������������жϣ�
�⣺��1��������һ����ǵ��ڡ�A��90����һ�룬�������Ϊ45����������Ϊ45����
��������A������������У���һ��������һ����һ�룬���н�С�Ľ�Ϊ��180����90��������1+2����30����
��ô�ϴ�Ľ�Ϊ60����
�ʴ�Ϊ��45����45����30����60����
��2���������������¼��������
������B��![]() ��C�����B��20����
��C�����B��20����
������C��![]() ��B�����B��80����
��B�����B��80����
������A��![]() ��C�����A��20������B��120����
��C�����A��20������B��120����
������C��![]() ��A�����A��80������B��60����
��A�����A��80������B��60����
������B��![]() ��A�����B����180����40������3��
��A�����B����180����40������3��![]() ��
��
������A��![]() ��B�����B����180����40������3��2��
��B�����B����180����40������3��2��![]() ��
��
��3����AB��CD��AD��BC����C��72����
��ABCD��ƽ���ı��Σ�
���C����A��72������D����ABC��180����72����108����
���۵��ã���C����BFE��72����
��BF��AD��
���AFB��90����
���DFE��180����90����72����18����
���DEF��180����108����18����54��
���DEF��![]() ��D��
��D��
���EDF�ǰ�������Σ�

 �����ƻ���ĩ��̶�100��ϵ�д�
�����ƻ���ĩ��̶�100��ϵ�д� �ܿ���ȫ��100��ϵ�д�
�ܿ���ȫ��100��ϵ�д�