Question

【题目】如图1，点为直线上一点，过点作射线，使，将一直角三角板的直角项点放在点处，一边在射线上，另一边在直线的下方.

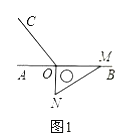
如图2,将图1中的三角板绕点逆时针旋转，使边在的内部，且恰好平分.此时__ 度;

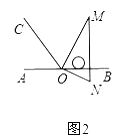
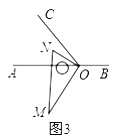
如图3,继续将图2中的三角板绕点按逆时针方向旋转，使得在的内部.试探究与之间满足什么等量关系，并说明理由;

将图1中的三角板绕点按每秒的速度沿逆时针方向旋转一周，在旋转的过程中，若第秒时，三条射线恰好构成相等的角，则的值为__ (直接写出结果).

Answer 1

【答案】（1）25°；（2）∠AOM-∠NOC=40°，理由详见解析；（3）t的值为13，34，49或64.

【解析】

（1）由平角的定义先求出∠BOC的度数，然后由角平分线的定义求出∠BOM的度数，再根据∠BON=∠MON-∠BOM可以求出结果；

（2）根据题意得出∠AOM+∠AON=90°①，∠AON+∠NOC=50°②，利用①-②可以得出结果；

（3）根据已知条件可知，在第t秒时，三角板转过的角度为5°t，然后按照OA、OC、ON三条射线构成相等的角分四种情况讨论，即可求出t的值.

解：（1）∵∠AOC=50°，

∴∠BOC=180°-∠AOC=130°，

∵OM平分∠BOC，∴∠BOM=∠BOC=55°，

∴∠BON=90°-∠BOM=25°.

故答案为：25；

（2）∠AOM与∠NOC之间满足等量关系为：∠AOM-∠NOC=40°，

理由如下：∵∠MON=90°，∠AOC=50°，

∴∠AOM+∠AON=90°①，∠AON+∠NOC=50°②，

∴①-②得，∠AOM-∠NOC=40°.

（3）∵三角板绕点O按每秒5°的速度沿逆时针方向旋转，
∴第t秒时，三角板转过的角度为5°t，

当三角板转到如图①所示时，∠AON=∠CON.
∵∠AON=90°+5°t，∠CON=∠BOC+∠BON=130°+90°-5°t=220°-5°t，
∴90°+5°t=220°-5°t，
即t=13；
当三角板转到如图②所示时，∠AOC=∠CON=50°，
∵∠CON=∠BOC-∠BON=130°-（5°t-90°）=220°-5°t，
∴220°-5°t=50°，
即t=34；
当三角板转到如图③所示时，∠AON=∠CON=∠AOC=25°，
∵∠CON=∠BON-∠BOC=（5°t-90°）-130°=5°t-220°，
∴5°t-220°=25°，
即t=49；
当三角板转到如图④所示时，∠AON=∠AOC=50°，
∵∠AON=5°t-180°-90°=5°t-270°，
∴5°t-270°=50°，
即t=64．

故t的值为13，34，49或64.