题目内容
【题目】已知△ABC中,∠C是其最小的内角,如果过点B的一条直线把这个三角形分割成了两个三角形,其中一个为等腰三角形,另一个为直角三角形,则称这条直线为△ABC关于点B的奇异分割线.
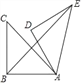
例如:图1,在Rt△ABC中,∠A=90°,∠C=20°,过顶点B的一条直线BD交AC于点D,且∠DBC=20°,则直线BD是△ABC的关于点B的奇异分割线.
(1)如图2,在△ABC中,若∠A=50°,∠C=20°.请过顶点B在图2中画出△ABC关于点B的奇异分割线BD交AC于点D,此时∠ADB= 度;
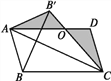
(2)在△ABC中,∠C=30°,若△ABC存在关于点B的奇异分割线,画出相应的△ABC及分割线BD,并直接写出此时∠ABC的度数(要求在图中标注∠A、∠ABD及∠DBC的度数).
【答案】(1)40;(2)∠ABC的值为60°或120°或105°
【解析】
(1)首先了解奇异分割线.的定义,然后把角ABC分成90°角和20°角即可;
(2)设BD为△ABC的奇异分割线.,分以下两种情况.第一种情况:△BDC是等腰三角形,△ABD是直角三角形;第二种情况:△BDC是直角三角形,△ABD是等腰三角形分别进行分析.
解:(1)如图所示:直线BD即为所求,此时∠ADB=90°﹣∠A=40°.
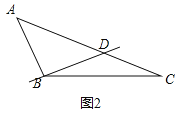
故答案为40.
(2)设BD为△ABC的奇异分割线,分以下两种情况.
第一种情况:△BDC是等腰三角形,△ABD是直角三角形,易知∠C和∠DBC必为底角,∴∠DBC=∠C=30°.
当∠A=90°时,△ABC存在奇异分割线,此时∠ABC=60°.
当∠ABD=90°时,△ABC存在奇异分割线,此时∠ABC=120°
当∠ADB=90°时,不符合题意.
第二种情况:△BDC是直角三角形,△ABD是等腰三角形,
当∠DBC=90°时,此时BD=AD,则△ABC存在奇异分割线,此时∠ABC=120°.
当∠BDC=90°时,此时BD=AD,则△ABC存在奇异分割线,此时∠ABC=105°
综上所述,满足条件的∠ABC的值为60°或120°或105°

 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案【题目】某市在今年对全市6000名八年级学生进行了一次视力抽样调查,并根据统计数据,制作了的统计表和如图所示统计图.
组别 | 视力 | 频数(人) |
A |
| 20 |
B |
| a |
C |
| b |
D |
| 70 |
E |
| 10 |
请根据图表信息回答下列问题:
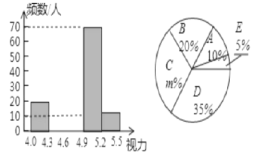
(1)求抽样调查的人数;
(2)![]() ______,
______,![]() ______,
______,![]() ______;
______;
(3)补全频数分布直方图;
(4)若视力在4.9以上(含4.9)均属正常,则视力正常的人数占被统计人数的百分比是多少?根据上述信息估计该市今年八年级的学生视力正常的学生大约有多少人?