题目内容
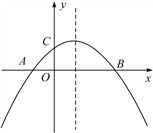
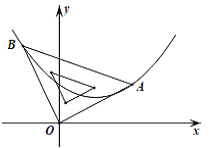
【题目】两幢大楼的部分截面及相关数据如图,小明在甲楼A处透过窗户E发现乙楼F处出现火灾,此时A,E,F在同一直线上.跑到一楼时,消防员正在进行喷水灭火,水流路线呈抛物线,在1.2m高的D处喷出,水流正好经过E,F. 若点B和点E、点C和F的离地高度分别相同,现消防员将水流抛物线向上平移0.4m,再向左后退了____m,恰好把水喷到F处进行灭火.

【答案】![]()
【解析】设直线AE的解析式为:y=kx+21.2.
把E(20,9.2)代入得,
20k+21.2=9.2,
∴k=-0.6,
∴y=-0.6x+21.2.
把y=6.2代入得,
-0.6x+21.2=6.2,
∴x=25,
∴F(25,6.2).
设抛物线解析式为:y=ax2+bx+1.2,
把E(20,9.2), F(25,6.2)代入得,
![]()
解之得
![]() ,
,
∴y=-0.04x2+1.2x+1.2,
设向上平移0.4m,向左后退了hm, 恰好把水喷到F处进行灭火由题意得
y=-0.04(x+h)2+1.2(x+h)+1.2+0.4,
把F(25,6.2)代入得,
6.2=-0.04×(25+h)2+1.2(25+h)+1.2+0.4,
整理得
h2+20h-10=0,
解之得
![]() ,
, ![]() (舍去).
(舍去).
∴向后退了![]() m
m

 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案【题目】盒中有若干枚黑棋和白棋,这些棋除颜色外无其他差别,现让学生进行摸棋试验:每次摸出一枚棋,记录颜色后放回摇匀,重复进行这样的试验得到以下数据:
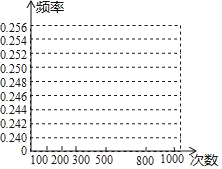
摸棋的次数n | 100 | 200 | 300 | 500 | 800 | 1000 |
摸到黑棋的次数m | 24 | 51 | 76 | b | 201 | 250 |
摸到黑棋的频率 | 0.240 | a | 0.253 | 0.248 | 0.251 | 0.250 |
(1)填空:a= ,b= ;
(2)在图中,画出摸到黑棋的折线统计图;
(3)随机摸一次,估计摸到黑棋的概率.(精确到0.01)