题目内容
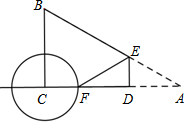
如图,在Rt△ABC中,∠C=90°,∠A=30°,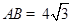 .若动点D在线段AC上(不与点A、C重合),过点D作DE⊥AC交AB边于点E.
.若动点D在线段AC上(不与点A、C重合),过点D作DE⊥AC交AB边于点E.
(1)当点D运动到线段AC中点时,DE= ;
(2)点A关于点D的对称点为点F,以FC为半径作⊙C,当DE= 时,⊙C与直线AB相切.
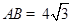 .若动点D在线段AC上(不与点A、C重合),过点D作DE⊥AC交AB边于点E.
.若动点D在线段AC上(不与点A、C重合),过点D作DE⊥AC交AB边于点E.(1)当点D运动到线段AC中点时,DE= ;
(2)点A关于点D的对称点为点F,以FC为半径作⊙C,当DE= 时,⊙C与直线AB相切.

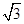 ;
;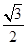 或
或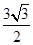
(1)求出BC,AC的值,推出DE为三角形ABC的中位线,求出即可;
(2)求出AB上的高,CH,即可得出圆的半径,证△ADE∽△ACB得出比例式,代入求出即可.
解:(1)∵∠C=90°,∠A=30°,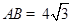 ,
,
∴BC=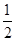 AB=
AB=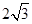 ,AC=6,
,AC=6,
∵∠C=90°,DE⊥AC,
∴DE∥BC,
∵D为AC中点,
∴E为AB中点,
∴DE=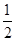 BC=
BC=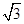 ,
,
故答案为: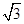 ;
;
(2)过C作CH⊥AB于H,
∵∠ACB=90°,BC=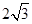 ,AB=
,AB=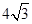 ,AC=6,
,AC=6,
∴由三角形面积公式得: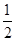 BC•AC=
BC•AC=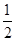 AB•CH, CH=3,
AB•CH, CH=3,
分为两种情况:
①如图1,

∵CF=CH=3,
∴AF=6﹣3=3,
∵A和F关于D对称,
∴DF=AD=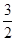 ,
,
∵DE∥BC,
∴△ADE∽△ACB,
∴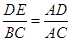 ,
,
∴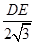 =
=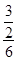 ,
,
DE=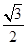 ;
;
②如图2,
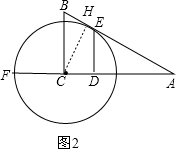
∵CF=CH=3,
∴AF=6+3=9,
∵A和F关于D对称,
∴DF=AD=4.5,
∵DE∥BC,
∴△ADE∽△ACB,
∴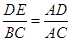 ,
,
∴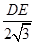 =
=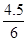 ,
,
DE=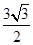 ;
;
故答案为: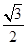 或
或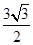
(2)求出AB上的高,CH,即可得出圆的半径,证△ADE∽△ACB得出比例式,代入求出即可.
解:(1)∵∠C=90°,∠A=30°,
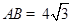 ,
,∴BC=
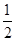 AB=
AB=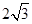 ,AC=6,
,AC=6,∵∠C=90°,DE⊥AC,
∴DE∥BC,
∵D为AC中点,
∴E为AB中点,
∴DE=
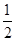 BC=
BC=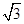 ,
,故答案为:
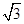 ;
;(2)过C作CH⊥AB于H,
∵∠ACB=90°,BC=
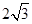 ,AB=
,AB=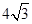 ,AC=6,
,AC=6,∴由三角形面积公式得:
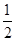 BC•AC=
BC•AC=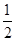 AB•CH, CH=3,
AB•CH, CH=3,分为两种情况:
①如图1,

∵CF=CH=3,
∴AF=6﹣3=3,
∵A和F关于D对称,
∴DF=AD=
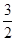 ,
,∵DE∥BC,
∴△ADE∽△ACB,
∴
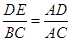 ,
,∴
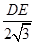 =
=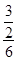 ,
,DE=
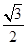 ;
;②如图2,

∵CF=CH=3,
∴AF=6+3=9,
∵A和F关于D对称,
∴DF=AD=4.5,
∵DE∥BC,
∴△ADE∽△ACB,
∴
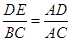 ,
,∴
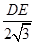 =
=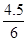 ,
,DE=
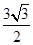 ;
;故答案为:
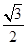 或
或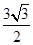

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
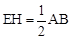 ;
;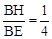 ,求
,求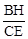 的值.
的值.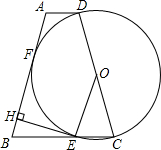
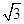 为半径作圆,点M(a,b) 是⊙P上的一点,则
为半径作圆,点M(a,b) 是⊙P上的一点,则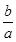 的最大值是 .
的最大值是 .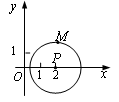

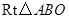 中,
中,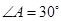 ,
,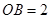 ,如果将
,如果将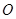 按顺时针方向旋转到
按顺时针方向旋转到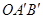 的位置.
的位置.
 的坐标.
的坐标. 从开始到
从开始到 点结束经过的路径长.
点结束经过的路径长.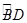 的中点,CE⊥AB于点E,BD交CE于点F.
的中点,CE⊥AB于点E,BD交CE于点F.