题目内容
【题目】如图所示,将矩形OABC置于平面直角坐标系中,点A,C分别在x,y轴的正半轴上,已知点B(4,2),将矩形OABC翻折,使得点C的对应点P恰好落在线段OA(包括端点O,A)上,折痕所在直线分别交BC、OA于点D、E;若点P在线段OA上运动时,过点P作OA的垂线交折痕所在直线于点 Q.设点Q的坐标为(x,y),则y关于x的函数关系式是 .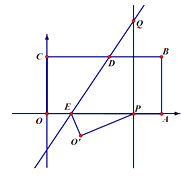
【答案】y = ![]() x2+1
x2+1
【解析】连接CQ,PQ交BD于点F,如图所示:
由折叠的性质得:CQ=PQ,
∵B(4,2),Q(x,y),
∴CF=x,QF=y-2,CQ=PQ=y,
又∵△CFQ为直角三角形,
∴CF2+QF2=CQ2,
∴x2+(y-2)2=y2,
∴y=![]() x2+1,
x2+1,
所以答案是:y=![]() x2+1.
x2+1.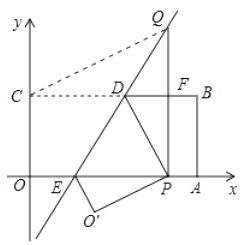
【考点精析】关于本题考查的函数关系式和勾股定理的概念,需要了解用来表示函数关系的数学式子叫做函数解析式或函数关系式;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能得出正确答案.

练习册系列答案
相关题目
【题目】某学习小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如下的表格,则符合这一结果的实验最有可能的是( )
实验次数 | 100 | 200 | 300 | 500 | 800 | 1000 | 2000 |
频率 | 0.365 | 0.328 | 0.330 | 0.334 | 0.336 | 0.332 | 0.333 |
A.一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃
B.在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
C.抛一个质地均匀的正六面体骰子,向上的面点数是5
D.抛一枚硬币,出现反面的概率