题目内容
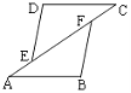
【题目】已知如图,A、E、F、C四点共线,BF=DE,AB=CD.
(1)请你添加一个条件,使△DEC≌△BFA;
(2)在(1)的基础上,求证:DE∥BF.
【答案】(1)添加的条件为:AE=CF(答案不唯一);(2)证明见解析;
【解析】
(1)添加的条件AE=CF,因此可得AF=CE,即可证明△DEC≌△BFA;
(2) 由(1)知△DEC≌△BFA,得到∠DEC=∠BFA,根据直线平行的判定,即可证明;
解:(1)添加的条件为:AE=CF,
证明:∵AE=CF,
∴AE+EF=CF+EF,
即:AF=CE,
又∵BF=DE,AB=CD,
∴在△DEC和△BFA中,
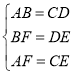
∴△DEC≌△BFA(SSS);
(2)由(1)知△DEC≌△BFA,
∴∠DEC=∠BFA
(全等三角形对应角相等),
∴DE∥BF(内错角相等,两直线平行).

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目