题目内容
【题目】已知二次函数 ![]() 的图像经过点
的图像经过点 ![]() .
.
(1)求这个二次函数的函数解析式;
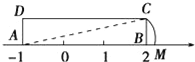
(2)若抛物线交x轴于A,B两点,交y轴于C点,顶点为D,求以A、B、C、D为顶点的四边形面积.
【答案】
(1)解:将 (2,![]() ) 代入 y=x2+bx
) 代入 y=x2+bx![]() ,得:
,得:
4+2b![]() =
=![]() ,
,
∴ b=1 ,
∴二次函数解析式为 y=x2x![]() .
.
(2)解:∵抛物线交x轴于A,B两点,
∴A(![]() ,0),B(
,0),B(![]() ,0),
,0),
又∵抛物线交交y轴于C点,
∴C(0,![]() ),
),
又∵抛物线顶点为D,
∴D(![]() ,1) .
,1) .
∴S四边形ABCD= ![]() ×
×![]() ×
×![]() +
+![]() ×(
×(![]() +1)×
+1)×![]() +
+![]() ×1×1=
×1×1=![]() .
.
【解析】(1)将(2,![]() )代入函数解析式求出b的值,从而得出函数解析式.
)代入函数解析式求出b的值,从而得出函数解析式.
(2)根据题意分别求出A、B、C、D点的坐标,用分割法求出四边形ABCD的面积.
【考点精析】解答此题的关键在于理解抛物线与坐标轴的交点的相关知识,掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.

练习册系列答案
相关题目