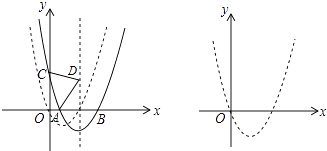题目内容
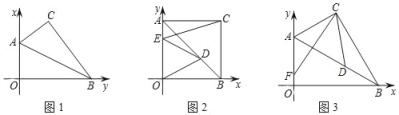
【题目】在平面直角坐标系中,点A(0,4),B(m,0)在坐标轴上,点C,O关于直线AB对称,点D在线段AB上.
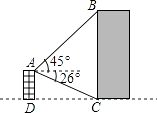
(1)如图1,若m=8,求AB的长;
(2)如图2,若m=4,连接OD,在y轴上取一点E,使OD=DE,求证:CE=![]() DE;
DE;
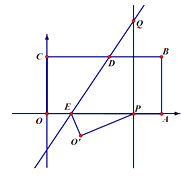
(3)如图3,若m=4![]() ,在射线AO上裁取AF,使AF=BD,当CD+CF的值最小时,请在图中画出点D的位置,并直接写出这个最小值.
,在射线AO上裁取AF,使AF=BD,当CD+CF的值最小时,请在图中画出点D的位置,并直接写出这个最小值.
【答案】(1)AB=4![]() ;(2)见解析;(3)CD+CF的最小值为4
;(2)见解析;(3)CD+CF的最小值为4![]() .
.
【解析】
(1)根据勾股定理可求AB的长;
(2)过点D作DF⊥AO,根据等腰三角形的性质可得OF=EF,根据轴对称的性质等腰直角三角形的性质可得AF=DF,设OF=EF=x,AE=4﹣2x,根据勾股定理用参数x表示
DE,CE的长,即可证CE=![]() DE;
DE;
(3)过点B作BM⊥OB,在BM上截取BM=AO,过点C作CN⊥BM,交MB的延长线于点N,根据锐角三角函数可得∠ABO=30°,根据轴对称的性质可得AC=AO=4,BO=BC=4![]() ,∠ABO=∠ABC=30°,∠OAB=∠CAB=60°,根据“SAS”可证△ACF≌△BMD,可得CF=DM,则当点D在CM上时,CF+CD的值最小,根据直角三角形的性质可求CN,BN的长,根据勾股定理可求CM的长,即可得CF+CD的最小值.
,∠ABO=∠ABC=30°,∠OAB=∠CAB=60°,根据“SAS”可证△ACF≌△BMD,可得CF=DM,则当点D在CM上时,CF+CD的值最小,根据直角三角形的性质可求CN,BN的长,根据勾股定理可求CM的长,即可得CF+CD的最小值.
(1)∵点A(0,4),B(m,0),且m=8,
∴AO=4,BO=8,
在Rt△ABO中,AB=![]()
(2)如图,过点D作DF⊥AO,
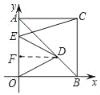
∵DE=DO,DF⊥AO,
∴EF=FO,
∵m=4,
∴AO=BO=4,
∴∠ABO=∠OAB=45°,
∵点C,O关于直线AB对称,
∴∠CAB=∠CBA=45°,AO=AC=OB=BC=4,
∴∠CAO=∠CBO=90°,
∵DF⊥AO,∠BAO=45°,
∴∠DAF=∠ADF=45°,
∴AF=DF,
设OF=EF=x,AE=4﹣2x,
∴AF=DF=4﹣x,
在Rt△DEF中,DE=![]()
在Rt△ACE中,CE=![]()
∴CE=![]() DE,
DE,
(3)如图,过点B作BM⊥OB,在BM上截取BM=AO,过点C作CN⊥BM,交MB的延长线于点N,
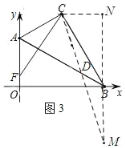
∵m=4![]() ,
,
∴OB=4![]() ,
,
∴tan∠ABO=![]() ,
,
∴∠ABO=30°
∵点C,O关于直线AB对称,
∴AC=AO=4,BO=BC=4![]() ,∠ABO=∠ABC=30°,∠OAB=∠CAB=60°,
,∠ABO=∠ABC=30°,∠OAB=∠CAB=60°,
∴∠CAF=120°,∠CBO=60°
∵BM⊥OB,∠ABO=30°,
∴∠ABM=120°,
∴∠CAF=∠ABM,且DB=AF,BM=AO=AC=4,
∴△ACF≌△BMD(SAS)
∴CF=DM,
∵CF+CD=CD+DM,
∴当点D在CM上时,CF+CD的值最小,
即CF+CD的最小值为CM的长,
∵∠CBO=60°,BM⊥OB,
∴∠CBN=30°,且BM⊥OB,BC=4![]() ,
,
∴CN=2![]() ,BN=
,BN=![]() CN=6,
CN=6,
∴MN=BM+BN=4+6=10,
在Rt△CMN中,CM=![]() ,
,
∴CD+CF的最小值为![]() .
.

 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案