题目内容
【题目】如图，把一个边长为
的大正方形，剪去一个边长为
的小正方形后，得到图①，称之为“前世”，然后再剪拼成一个新长方形即图②，称之为“今生”，请你解答下面的问题：
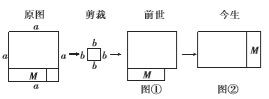
（1）“前世”图①的面积与“今生”图②新长方形的面积______；
（2）根据图形面积的和差关系直接写出“前世”图①的面积为_______，标明“今生”图②新长方形的长为______、宽为_______、面积为_______；
（3）“形缺数时少直观，数缺形时少形象”它体现了数学的数形结合思想，由（1）和（2）图形面积的计算，形象地验证了代数中的一个乘法公式：______；
（4）利用本题所得公式计算：
．
【答案】（1）相等；（2）a2-b2，a+b，a-b，（a+b）（a-b）；（3）a2-b2=（a+b）（a-b）；（4）3.999999．
【解析】
（1）根据图形的变化规律即可解决问题；
（2）观察图形即可解决问题；
（3）由（1）（2）可得结论；
（4）利用公式：a2-b2=（a+b）（a-b）即可解决问题；
（1）由题意可知：前世”图①的面积与“今生”图②新长方形的面积相等，
故答案为相等．
（2）根据图形面积的和差关系直接写出“前世”图①的面积为：a2-b2，标明“今生”图②新长方形的长为a+b、宽为a-b，面积为：（a+b）（a-b）．
故答案为a2-b2，a+b，a-b，（a+b）（a-b）；
（3）“形缺数时少直观，数缺形式少形象”它体现了数学的数形结合思想，由（1）和（2）图形面积的计算，形象的验证了代数中的一个乘法公式为：a2-b2=（a+b）（a-b）．
故答案为a2-b2=（a+b）（a-b）
（4）2.001×1.999=（2+0.001）（2-0.001）=22-（0.001）2=4-0.000001=3.999999．
