题目内容
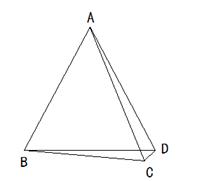
如图1所示,已知在△ABC和△DEF中, 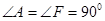 ,
,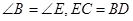 .
.
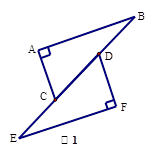
(1)试说明:△ABC≌△FED的理由;
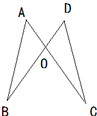
(2)若图形经过平移和旋转后得到如图2,若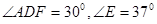 ,试求∠DHB的度数;
,试求∠DHB的度数;
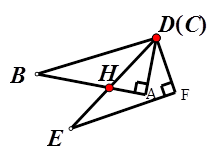
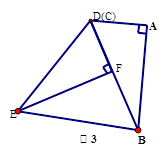
(3)若将△ABC继续绕点D旋转后得到图3,此时D、B、F三点在同一条直线上,若DF:FB=3:2,连结EB,已知△ABD的周长是12,且AB-AD=1,你能求出四边形ABED的面积吗?若能,请求出来;若不能,请说明理由。
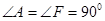 ,
,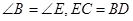 .
.
(1)试说明:△ABC≌△FED的理由;
(2)若图形经过平移和旋转后得到如图2,若
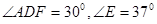 ,试求∠DHB的度数;
,试求∠DHB的度数;
(3)若将△ABC继续绕点D旋转后得到图3,此时D、B、F三点在同一条直线上,若DF:FB=3:2,连结EB,已知△ABD的周长是12,且AB-AD=1,你能求出四边形ABED的面积吗?若能,请求出来;若不能,请说明理由。

(1)见解析;(2)113°;(3)16
试题分析:(1)由
 可得BC=ED,再有
可得BC=ED,再有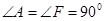 ,
,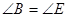 ,即可证得结论;
,即可证得结论;(2)根据旋转的性质及三角形的内角和定理即可求得结果;
(3)设AD的长为
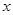 ,AB的长为
,AB的长为 ,则
,则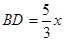 ,根据△ABD的周长是12,且AB-AD=1,即可列出方程组解出x、y,再由△ABD≌△FED可得EF的长,最后根据
,根据△ABD的周长是12,且AB-AD=1,即可列出方程组解出x、y,再由△ABD≌△FED可得EF的长,最后根据 即得结果.
即得结果.(1)

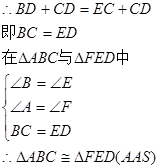
(2)由题意可得
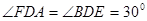
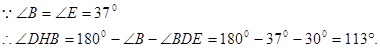
(3)设AD的长为
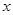 ,AB的长为
,AB的长为 ,则
,则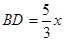 ,由题意得
,由题意得 ,
,
即AD=3,AB=4,BD=5
∵△ABD≌△FED,
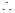 EF=AB=4
EF=AB=4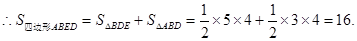
点评:解答本题的关键是熟练掌握平移和旋转的基本性质,准确把握旋转角,在做第三问时要读懂题意,准确把握题中量与量之间的关系,正确列出方程组.

练习册系列答案
相关题目
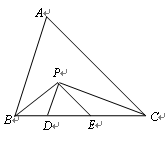
 中,
中, 是
是 ,
, 平分线的交点,
平分线的交点, ,
, ,
, ,
, ,求
,求 的周长.
的周长.


 ,则这个多边形是 边形.
,则这个多边形是 边形.