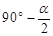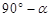题目内容
在 中,
中, 是
是 ,
, 平分线的交点,
平分线的交点, ,
,
(1)求证: ,
,
(2)若 ,
, ,求
,求 的周长.
的周长.
 中,
中, 是
是 ,
, 平分线的交点,
平分线的交点, ,
,(1)求证:
 ,
,(2)若
 ,
, ,求
,求 的周长.
的周长.
(1)见解析;(2)17
试题分析:根据
 是角平分线可得
是角平分线可得 ,再由
,再由 可得
可得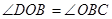 ,从而可得
,从而可得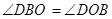 ,根据等边对等角即可得到
,根据等边对等角即可得到 ,同理可证
,同理可证 ,即可得到结果。
,即可得到结果。 
 是角平分线,
是角平分线,∴
 ,
,又
 ,
,∴
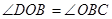 ,
,∴
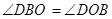 ,
,∴
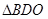 是等腰三角形,
是等腰三角形,∴
 ,
,同理可证
 ,
, ∴
 ,
,∴周长为:
 .
.点评:在一个问题中角平分线和平行线同时出现时,往往能够得到等腰三角形,希望同学们熟练掌握这一特征。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
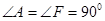 ,
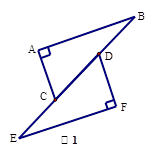
,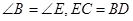 .
.
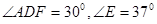 ,试求∠DHB的度数;
,试求∠DHB的度数;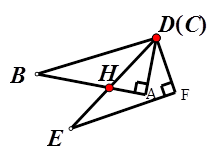

 ,则它一腰上的高与底边的夹角等于( )
,则它一腰上的高与底边的夹角等于( )