题目内容
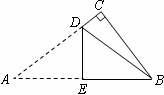
如图,在△ABC中,AB=AC,∠ABD=60°,∠ABC >60°,2∠ADB=180°-∠BDC.
求证:AB=BD+DC.
求证:AB=BD+DC.

见解析
试题分析:延长CD至E,使DE=DB,连接AE,由2∠ADB=180°-∠BDC可得∠ADB=∠ADE,即可证得△ABD≌△ADE,得到AB=AE,∠E=∠ABD=60°,从而可证得△ADE是等边三角形,即可证得结论.
如图,延长CD至E,使DE=DB,连接AE
∵2∠ADB=180°-∠BDC
∴∠ADB=∠ADE
在△ABD和△ADE中
AD=AD,∠ADB=∠ADE,DB=DE
∴△ABD≌△ADE(SAS)
∴AB=AE,∠E=∠ABD=60°
∵AB=AC
∴AE=AC
∴△ADE是等边三角形
∴CE=AC=AB
∵CE=DC+DE=DC+DB
∴AB=DC+DB.
点评:解答本题的关键是正确作出辅助线,同时熟记有一个角是60°的等腰三角形是等边三角形.

练习册系列答案
相关题目
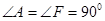 ,
,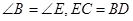 .
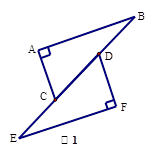
.
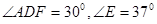 ,试求∠DHB的度数;
,试求∠DHB的度数;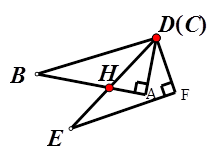
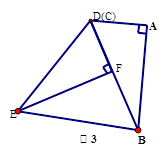
 中,
中, ,
,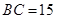 ,斜边
,斜边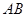 的垂直平分线与
的垂直平分线与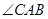 的平分线都交
的平分线都交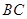 于
于 点,则点
点,则点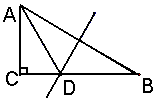
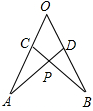

 中,
中,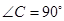 ,
,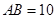 cm,
cm,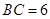 cm.现将
cm.现将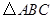 沿折痕
沿折痕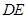 进行折叠,使顶点
进行折叠,使顶点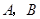 重合,则
重合,则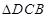 的周长等于 cm.
的周长等于 cm.