Question

【题目】如图1，点是直线上一点，点是直线上一点，且MN//PQ．和的平分线交于点．

（1）求证：；

（2）过点作直线交于点（不与点重合），交于点E,

①若点在点的右侧，如图2，求证：；

②若点在点的左侧，则线段、、有何数量关系？直接写出结论，不说理由．

Answer 1

【答案】（1）见解析；（2）见解析；（3）

【解析】

(1) 由平行线性质可得∠NAB+∠ABQ=180°,再由角平分线定义可得,再利用三角形内角和定理即可得∠C=90°,即可证明BC⊥AC;

(2) ①延长AC交PQ点F，先证明AC=FC,再证明△ACD≌△FCE,即可得AD+BE=AB;

②方法与①相同．

解：（1）∵MN∥PQ

∴∠NAB+∠ABQ=180°

∵AC平分∠NAB，BC平分∠ABQ

∴

∴∠BAC+∠ABC==90°

在△ABC中，∵∠BAC+∠ABC+∠C=180°

∴∠C=180°- (∠BAC+∠ABC) =180°-90°=90°

∴BC⊥AC;

（2）①延长AC交PQ于点F

∵BC⊥AC

∴∠ACB=∠FCB=90°

∵BC平分∠ABF

∴∠ABC=∠FBC

∴BC=BC

∴△ABC≌△FBC

∴AC=CF，AB=BF

∵MN∥BQ

∴∠DAC=∠EFC

∵∠ACD=∠FCE

∴△ACD≌△FCE

∴AD=EF

∴AB=BF=BE+EF=BE+AD

即：AB=AD+BE

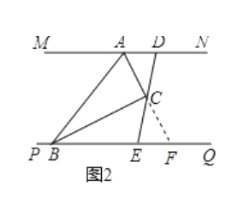
②线段AD，BE，AB数量关系是：AD+AB=BE

如图3，延长AC交PQ点F,

∵MN//PQ ．

∴∠AFB=∠FAN，∠DAC=∠EFC

∵AC平分∠NAB

∴∠BAF=∠FAN

∴∠BAF=∠AFB

∴AB=FB

∵BC⊥AC

∴C是AF的中点

∴AC=FC

在△ACD与△FCE中

∴

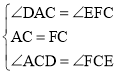
∴AD=EF

∵AB=FB=BE-EF

∴AD+AB=BE