题目内容
【题目】有三张卡片（形状、大小、颜色、质地都相等），正面分别写上整式x2+1，﹣x2﹣2，3．将这三张卡片背面向上洗匀，从中任意抽取一张卡片，记卡片上的整式为A，再从剩下的卡片中任意抽取一张，记卡片上的整式为B，于是得到代数式 
．
（1）请用画树状图或列表的方法，写出代数式 所有可能的结果；
（2）求代数式 恰好是分式的概率．
【答案】
（1）解：画树状图：
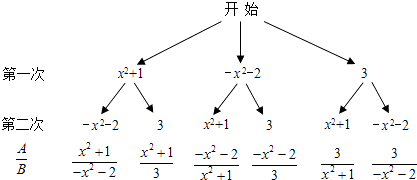
列表：
第一次 第二次 | x2+1 | ﹣x2﹣2 | 3 |
x2+1 |
|
| |
﹣x2﹣2 |
|
| |
3 |
|
|
（2）解：代数式 
所有可能的结果共有6种，其中代数式 是分式的有4种： 
， 
， 
， 
，
所以P （是分式）= 
．
【解析】（1）根据画树状图和列表，得到 所有可能的结果共有6种；（2）由（1）知代数式 所有可能的结果共有6种，其中代数式是分式的有4种，所以P
=
．
【考点精析】掌握列表法与树状图法和分式的概念及特征是解答本题的根本，需要知道当一次试验要设计三个或更多的因素时，用列表法就不方便了，为了不重不漏地列出所有可能的结果，通常采用树状图法求概率；整式A除以整式B，如果除式B中含有分母，那么这个就是分式，其中A叫分子，B叫分母．
【题目】近年来，共享单车逐渐成为高校学生喜爱的“绿色出行”方式之一，自2016年国庆后，许多高校均投放了使用手机支付就可随取随用的共享单车．某高校为了解本校学生出行使用共享单车的情况，随机调查了某天部分出行学生使用共享单车的情况，并整理成如下统计表．
使用次数 | 0 | 1 | 2 | 3 | 4 | 5 |
人数 | 11 | 15 | 23 | 28 | 18 | 5 |
（1）这天部分出行学生使用共享单车次数的中位数是 ，众数是 ，该中位数的意义是 ；
（2）这天部分出行学生平均每人使用共享单车约多少次？（结果保留整数）
（3）若该校某天有1500名学生出行，请你估计这天使用共享单车次数在3次以上（含3次）的学生有多少人？
