Question

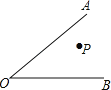
【题目】如图，P为∠AOB内一定点，M、N分别是射线OA、OB上一点，当△PMN周长最小时，∠OPM＝50°，则∠AOB＝（　　）

A.40°B.45°C.50°D.55°

Answer 1

【答案】A

【解析】

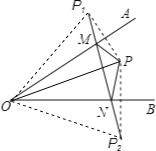
作P关于OA，OB的对称点P1，P2．连接OP1，OP2．则当M，N是P1P2与OA，OB的交点时，△PMN的周长最短，根据对称的性质可以证得：∠OP1M＝∠OPM＝50°，OP1＝OP2＝OP，根据等腰三角形的性质即可求解．

解：作P关于OA，OB的对称点P1，P2．连接OP1，OP2．则当M，N是P1P2与OA，OB的交点时，△PMN的周长最短，连接P1O、P2O，

∵PP1关于OA对称，

∴∠P1OP＝2∠MOP，OP1＝OP，P1M＝PM，∠OP1M＝∠OPM＝50°

同理，∠P2OP＝2∠NOP，OP＝OP2，

∴∠P1OP2＝∠P1OP+∠P2OP＝2（∠MOP+∠NOP）＝2∠AOB，OP1＝OP2＝OP，

∴△P1OP2是等腰三角形．

∴∠OP2N＝∠OP1M＝50°，

∴∠P1OP2＝180°﹣2×50°＝80°，

∴∠AOB＝40°，

故选：A．