题目内容
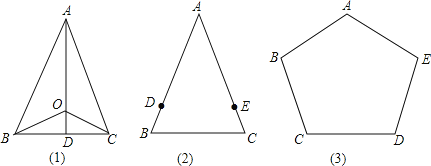
【题目】如图,在△ABC中,∠BAC=90°,AD⊥BC于点D,BE交AD于点F,交AC于点E,若BE平分∠ABC,试判断△AEF的形状,并说明理由.

【答案】△AEF为等腰三角形,理由见解析
【解析】
由在△ABC中,∠BAC=90°,AD⊥BC,易得∠BAD=∠C,又由BE平分∠ABC,∠AFE=∠ABF+∠BAD,∠AEF=∠CBE+∠C,即可证得∠AFE=∠AEF,继而证得:△AEF为等腰三角形.
解:△AEF为等腰三角形,
理由:∵在△ABC中,∠BAC=90°,AD⊥BC,
∴∠BAD+∠CAD=90°,∠CAD+∠C=90°,
∴∠BAD=∠C,
∵BE平分∠ABC,
∴∠3=∠4,
∵∠1=∠3+∠BAD,∠2=∠4+∠C,
∴∠1=∠2,
∴AF=AE,
即△AEF为等腰三角形.

练习册系列答案
相关题目
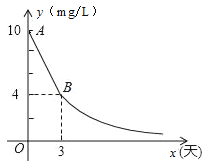
【题目】环保局对某企业排污情况进行检测,结果显示:所排污水中硫化物的浓度超标,即硫化物的浓度超过最高允许的1.0 mg/L.环保局要求该企业立即整改,在15天以内(含15天)排污达标.整改过程中,所排污水中硫化物的浓度y(mg/L)与时间x(天)的变化规律如图所示,其中线段AB表示前3天的变化规律,其中第3天时硫化物的浓度降为4 mg/L.从第3天起所排污水中硫化物的浓度y与时间x满足下面表格中的关系:
时间x(天) | 3 | 4 | 5 | 6 | 8 | …… |
硫化物的浓y(mg/L) | 4 | 3 | 2.4 | 2 | 1.5 |
(1)求整改过程中当0≤x<3时,硫化物的浓度y与时间x的函数表达式;
(2)求整改过程中当x≥3时,硫化物的浓度y与时间x的函数表达式;
(3)该企业所排污水中硫化物的浓度,能否在15天以内不超过最高允许的1.0 mg/L?为什么?