题目内容
【题目】如图,CD⊥AB于D,点F是BC上任意一点,FE⊥AB于E,且∠1=∠2,∠3=80°. 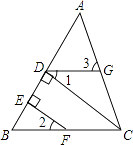
(1)试证明∠B=∠ADG;
(2)求∠BCA的度数.
【答案】
(1)证明:∵CD⊥AB,FE⊥AB,
∴CD∥EF,
∴∠2=∠BCD,
∵∠1=∠2,
∴∠1=∠BCD,
∴BC∥DG,
∴∠B=∠ADG
(2)解:∵DG∥BC,
∴∠3=∠BCG,
∵∠3=80°,
∴∠BCA=80°
【解析】(1)由CD⊥AB,FE⊥AB,则CD∥EF,则∠2=∠BCD,从而证得BC∥DG,即∠B=∠ADG;(2)由CD∥EF,则∠3=∠BCG.
【考点精析】认真审题,首先需要了解平行线的判定与性质(由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质).

练习册系列答案
相关题目
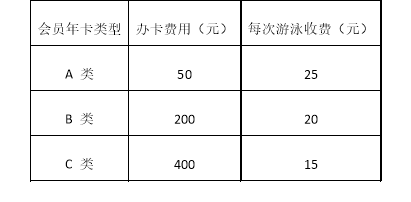
【题目】甲、乙两班举行电脑汉字输入比赛,参赛学生每分钟输入汉字的个数统计结果如下表:
班级 | 参赛人数 | 中位数 | 方差 | 平均数 |
甲 | 55 | 149 | 191 | 135 |
乙 | 55 | 151 | 110 | 135 |
某同学分析上表后得出如下结论:
①甲、乙两班学生成绩平均水平相同;
②乙班优秀的人数多于甲班优秀的人数(每分钟输入汉字≥150个为优秀);
③甲班成绩的波动比乙班大,
上述结论正确的是( )
A.①②③
B.①②
C.①③
D.②③