题目内容
【题目】如图,点M,N分别是正五边形ABCDE的边BC,CD上的点,且BM=CN,AM交BN于点P,则∠APN的度数为( ) 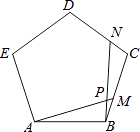
A.120°
B.118°
C.110°
D.108°
【答案】D
【解析】:∵五边形ABCDE为正五边形, ∴AB=BC,∠ABM=∠C,
在△ABM和△BCN中, 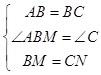
∴△ABM≌△BCN(SAS),
∴∴∠BAM=∠CBN,
∵∠BAM+∠ABP=∠APN,
∴∠CBN+∠ABP=∠APN=∠ABC= ![]() =108°,
=108°,
∴∠APN的度数为108°;
故选:D.
【考点精析】通过灵活运用多边形内角与外角和正多边形和圆,掌握多边形的内角和定理:n边形的内角和等于(n-2)180°.多边形的外角和定理:任意多边形的外角和等于360°;圆的内接四边形的对角互补,并且任何一个外角都等于它的内对角;圆的外切四边形的两组对边的和相等即可以解答此题.

练习册系列答案
相关题目