ĖâÄŋÄÚČÝ
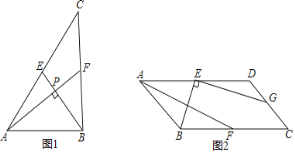
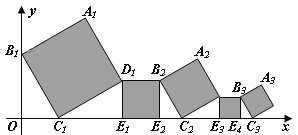
ĄūĖâÄŋĄŋÔÚĘýŅ§ŋÎÉÏĢŽžŨĄĒŌŌĄĒąûĄĒķĄËÄÎŧÍŽŅ§đēÍŽŅÐūŋķþīΚŊĘýyĢ―x2Đ2x+cĢĻcĘĮģĢĘýĢĐĢŪžŨ·ĒÏÖĢšļÚŊĘýĩÄÍžÏóÓëxÖáĩÄŌŧļö―ŧĩãĘĮĢĻĐ2ĢŽ0ĢĐĢŧŌŌ·ĒÏÖĢšļÚŊĘýĩÄÍžÏóÓëyÖáĩÄ―ŧĩãÔÚĢĻ0ĢŽĐ4ĢĐÉÏ·―Ģŧąû·ĒÏÖĢšÎÞÂÛxČĄČΚÎÖĩËųĩÃĩ―ĩÄyÖĩŨÜÄÜÂúŨãcĐyĄÜ1ĢŧķĄ·ĒÏÖĢšĩąĐ1ĢžxĢž0ĘąĢŽļÚŊĘýĩÄÍžÏóÔÚxÖáĩÄÏ·―ĢŽĩą3ĢžxĢž4ĘąĢŽļÚŊĘýĩÄÍžÏóÔÚxÖáĩÄÉÏ·―ĢŪÍĻđýĀÏĘĶĩÄŨîšóÆĀÅÐĩÃÖŠÕâËÄÎŧÍŽŅ§ÖÐÖŧÓÐŌŧÎŧÍŽŅ§·ĒÏÖĩÄ―áÂÛĘĮīíÎóĩÄĢŽÔōļÃÍŽŅ§ĘĮĢĻĄĄĄĄĢĐ
A. žŨB. ŌŌC. ąûD. ķĄ
Ąūīð°ļĄŋA
Ąū―âÎöĄŋ
ÓÉžŨĩÃĩ―yĢ―x22x8ĢŽÓÉŌŌĩÃĩ―yĢ―x22x4ĢŽËųŌÔËûÁĐąØÓÐŌŧļöīíÎóĢŽļųūÝķĄĩÄÐÅÏĒšŊĘýÓëxÖáĩÄÁ―ļö―ŧĩãxĢū1ĢŽxĢž3ĢŽžīŋÉĮó―âĢŧ
ļųūÝžŨĩÄÐÅÏĒĩÃĩ―cĢ―Đ8ĢŽ
ĄāyĢ―x2Đ2xĐ8ĢŽ
ÓëxÖáĩÄ―ŧĩãΊxĢ―4ĢŽxĢ―Đ2Ģŧ
ļųūÝŌŌĩÄÐÅÏĒĩÃĩ―cĢ―Đ4ĢŽ
ĄāyĢ―x2Đ2xĐ4ĢŽ
ÓëxÖáĩÄ―ŧĩãΊxĢ―1+![]() ĢŽxĢ―1Đ
ĢŽxĢ―1Đ![]() ĢŽ
ĢŽ
ļųūÝąûĩÄÐÅÏĒyĢ―ĢĻxĐ1ĢĐ2+cĐ1ĢŽ
šŊĘýÓÐŨîÐĄÖĩcĐ1ĢŽ
ĄāyĄÝcĐ1ĢŽ
đĘąûÕýČ·Ģŧ
ļųūÝķĄĩÄÐÅÏĒĩÃĩ―ĢŽšŊĘýÓëxÖáĩÄÁ―ļö―ŧĩãxĢūĐ1ĢŽxĢž3ĢŽ
ĄßÖŧÓÐŌŧļöīíÎóĢŽžŨŌŌŧĨÏāÃŽķÜĢŽŌŧķĻĘĮËûÁĐÖÐŌŧļöīíÎóĢŽ
ļųūÝķĄĖáđĐĩÄÐÅÏĒĢŽŋÉŌÔķÏķĻžŨīíÎóĢŧ
đĘŅĄĢšAĢŪ

 ÖąÍĻđóÖÝÃûÐĢÖÜēâÔÂŋžÖąÍĻÃûÐĢÏĩÁÐīð°ļ
ÖąÍĻđóÖÝÃûÐĢÖÜēâÔÂŋžÖąÍĻÃûÐĢÏĩÁÐīð°ļĄūĖâÄŋĄŋÄģģŽĘÐÏúĘÛŌŧÖÖÉĖÆ·ĢŽģÉąūÃŋĮ§ŋË40ÔŠĢŽđæķĻÃŋĮ§ŋËĘÛžÛēŧĩÍÓÚģÉąūĢŽĮŌēŧļßÓÚ80ÔŠĢŽūĘÐģĄĩũēéĢŽÃŋĖėĩÄÏúĘÛÁŋyĢĻĮ§ŋËĢĐÓëÃŋĮ§ŋËĘÛžÛxĢĻÔŠĢĐÂúŨãŌŧīΚŊĘýđØÏĩĢŽēŋ·ÖĘýūÝČįÏÂąíĢš
ĘÛžÛxĢĻÔŠ/Į§ŋËĢĐ | 50 | 60 | 70 |
ÏúĘÛÁŋyĢĻĮ§ŋËĢĐ | 100 | 80 | 60 |
ĢĻ1ĢĐĮóyÓëxÖŪžäĩÄšŊĘýąíīïĘ―Ģŧ
ĢĻ2ĢĐÉčÉĖÆ·ÃŋĖėĩÄŨÜĀûČóΊWĢĻÔŠĢĐĢŽÔōĩąĘÛžÛxķĻΊķāÉŲÔŠĘąĢŽģ§ÉĖÃŋĖėÄÜŧņĩÃŨîīóĀûČóĢŋŨîīóĀûČóĘĮķāÉŲĢŋ
ĢĻ3ĢĐČįđûģŽĘÐŌŠŧņĩÃÃŋĖėēŧĩÍÓÚ1350ÔŠĩÄĀûČóĢŽĮŌ·ûšÏģŽĘÐŨÔžšĩÄđæķĻĢŽÄĮÃīļÃÉĖÆ·ÃŋĮ§ŋËĘÛžÛĩÄČĄÖĩ·ķΧĘĮķāÉŲĢŋĮëËĩÃũĀíÓÉĢŪ