��Ŀ����
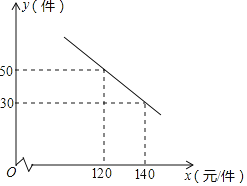
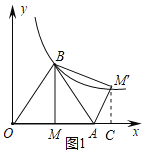
����Ŀ����ͼ1������������![]() (k>0)ͼ���ȱߡ�OAB��һ������B����A����Ϊ��2��0��������B��BM��x�ᣬ����ΪM��
(k>0)ͼ���ȱߡ�OAB��һ������B����A����Ϊ��2��0��������B��BM��x�ᣬ����ΪM��
��1�����B�������k��ֵ��
��2��������ABM��ֱ��AB���ۣ��õ���ABM'���жϸ÷���������ͼ���Ǵӵ�M'���Ϸ����������Ǵӵ�M'���·��������ֻ���ǡ�þ�����M'����˵�����ɣ�
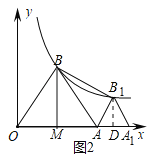
��3����ͼ2����x����ȡһ��A1����AA1Ϊ�߳����ȱߡ�AA1B1��ǡ��ʹ��B1���ڸ÷���������ͼ���ϣ�����BB1�����ABB1�������

���𰸡���1��k��![]() ����2���÷���������ͼ���Ǵӵ�M'���·����������ɼ���������3����ABB1�����Ϊ
����2���÷���������ͼ���Ǵӵ�M'���·����������ɼ���������3����ABB1�����Ϊ![]() .
.
��������
��1������OABΪ�ȱ������μ�OA��2���ɵó�OM��BM�ij��������ɵó���B�����꣬�ɵ�B���������÷���������ͼ���ϵ���������������k��ֵ��
��2������M����M��C��x�ᣬ����Ϊ��C�����۵������ʣ���֪��AM����AM��1����BAM������BAM��60������Rt��ACM���У�ͨ����ֱ�������ο����AC��CM���ij��������ɵó�OC�ij������÷���������ͼ���ϵ�������������������������ͼ����ֱ��CM������������꣬�������M����������ȽϺɵó����ۣ�
��3������B1��B1D��x�ᣬ����Ϊ��D����AA1��a����AD��![]() a��B1D��
a��B1D��![]() a��OD��2��
a��OD��2��![]() a�������ɵó���B1�����꣬���÷���������ͼ���ϵ���������������a��ֵ�������ɵó�MD��B1D��AD�ij����ٽ��S��ABB1��S����BMDB1S��BMAS��ADB1���������ABB1�������
a�������ɵó���B1�����꣬���÷���������ͼ���ϵ���������������a��ֵ�������ɵó�MD��B1D��AD�ij����ٽ��S��ABB1��S����BMDB1S��BMAS��ADB1���������ABB1�������
��1���ߡ�OABΪ�ȱ������Σ�OA��2��
��OM��![]() OA��1��BM��
OA��1��BM��![]() OA��
OA��![]() ��
��
���B��������1��![]() ����
����
�߷���������![]() ͼ����B��
ͼ����B��
��k��![]() ��
��
��2���÷���������ͼ���Ǵӵ�M'���·��������������£�
����M����M��C��x�ᣬ����Ϊ��C����ͼ1��ʾ��
���۵������ʣ���֪��AM����AM��1����BAM������BAM��60����
���M��AC��180������BAM����BAM����60����
��Rt��ACM����AM����1����ACM����90������M��AC��60����
���AM��C��30����
��AC��![]() AM����
AM����![]() ��CM����
��CM����![]() AM����
AM����![]() ��
��
��OC��OA+AC��![]() ��
��
���M����������![]() ��
��![]() ����
����
��x��![]() ʱ��
ʱ��![]() ��
��
��![]() ��
��![]() ��
��
��÷���������ͼ���Ǵӵ�M'���·�������
��3������B1��B1D��x�ᣬ����Ϊ��D����ͼ2��ʾ��
��AA1��a����AD��![]() a��B1D��
a��B1D��![]() a��OD��2+
a��OD��2+![]() a��
a��
���B1��������2+![]() a��
a��![]() a����
a����
�ߵ�B1�ڸ÷���������![]() ��ͼ���ϣ�
��ͼ���ϣ�
�ࣨ2+![]() a��
a��![]() a��
a��![]() ��
��
��ã�a1����2![]() ��2����ȥ����a2��2
��2����ȥ����a2��2![]() ��2��
��2��
��MD��AM+AD��![]() ��B1D��
��B1D��![]() a��
a��![]() ��
��![]() ��AD��
��AD��![]() a��
a��![]() ��1��
��1��
��S��ABB1��S����BMDB1S��BMAS��ADB1
��![]() ��BM+B1D��MD��
��BM+B1D��MD��![]() BMAM��
BMAM��![]() B1DAD��
B1DAD��
![]() ��
��
![]() .
.

 ��У����ϵ�д�
��У����ϵ�д�