��Ŀ����
����Ŀ��ij����С����һ����Ϊ���Ϸ���ľ���¥���þ���¥��һ¥�Ǹ�5��С�����У����������Ǿ���ס�����ڸ�¥��ǰ��15�״�Ҫ��һ����20����¥�������������������ˮƽ�ߵļн�Ϊ32��ʱ��
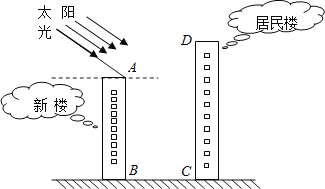
��1���ʳ������ϵľ���ס���ɹ��Ƿ���Ӱ�죬Ϊʲô��
��2����Ҫʹ���вɹⲻ��Ӱ�죬��¥Ӧ�������ף�����������������ο����ݣ�sin32���![]() ��cos32���
��cos32���![]() ��tan32���
��tan32���![]() ����
����
���𰸡���1����Ӱ�죬����������2��Ҫʹ���вɹⲻ��Ӱ�죬��¥Ӧ���32�ף�
��������
��1���������Ǻ��������������յ�����¥��ʲô�߶ȣ���5���бȽϣ�
��2�����в���Ӱ�죬˵��32��������Ӧ���䵽¥�ĵײ�C����������¥�ĸ߶Ⱥ�32��������ֵ���ɼ��㣮
�⣺��1����Ӱ��
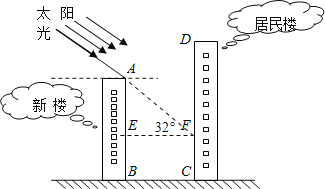
��RT��AEF��tan��AFE��tan32����![]() ��
��
��ã�AE��![]() ��
��
�ʿɵ�EB��![]() ��
��
���������ϵľ���ס���ɹ�Ҫ��Ӱ�죮
��2��Ҫʹ�ɹⲻ��Ӱ�죬˵��32��������Ӧ���䵽¥�ĵײ�C����
��tan32����![]() ��
��
��ã�EF��32�ף�
��Ҫʹ���вɹⲻ��Ӱ�죬��¥Ӧ���32�ף�

��ϰ��ϵ�д�
�����Ŀ