ЬтФПФкШн
ЁОЬтФПЁПЮЊКыбяДЋЭГЮФЛЏЃЌФГаЃОйааЁАаЃдАУегяДѓШќЁБЃЌБШШќНсЪјКѓ,зщжЏепНЋЫљгаВЮШќбЁЪжЕФБШШќГЩМЈ(ЕУЗжОљЮЊ5ЕФБЖЪ§)НјааећРэ,ВЂЗжБ№ЛцжЦГЩЩШаЮЭГМЦЭМКЭЦЕЪ§жБЗНЭМЃЌВПЗжаХЯЂШчЯТ:
(1)БОДЮБШШќВЮШќбЁЪжЙВга ШЫЃЌЦфжа![]() Зжга ШЫЃЌ
Зжга ШЫЃЌ![]() Зжга ШЫЃЛ
Зжга ШЫЃЛ
(2)ШќЧАЙцЖЈ,ГЩМЈДяЕНЦНОљЗжЕФВЮШќбЁЪжМДПЩЛёНБ.ФГВЮШќбЁЪжЕФБШШќГЩМЈЮЊ75Зж,ЪдХаЖЯЫћФмЗёЛёНБ,ВЂЫЕУїРэгЩЃЛ
(3)ГЩМЈЧАЫФУћЪЧ2УћФаЩњКЭ2УћХЎЩњ,ШєДгЫћУЧжаШЮбЁ2ШЫзїЮЊЛёНБДњБэЗЂбд,ЪдЧѓЧЁКУбЁжа1Фа1ХЎЕФИХТЪ.
ЁОД№АИЁПЃЈ1ЃЉ50ЃЌ![]() ЃЌ
ЃЌ![]() ЃЛЃЈ2ЃЉЫћПЩвдЛёНБЃЛРэгЩМћНтЮіЃЛЃЈ3ЃЉ
ЃЛЃЈ2ЃЉЫћПЩвдЛёНБЃЛРэгЩМћНтЮіЃЛЃЈ3ЃЉ![]() .
.
ЁОНтЮіЁП
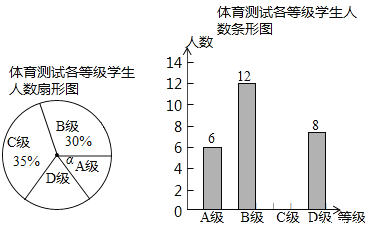
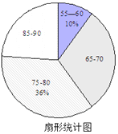
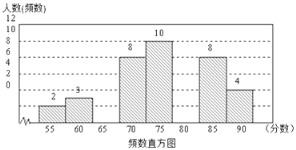
ЃЈ1ЃЉгУЁА55ЁЋ60ЁБетзщЕФШЫЪ§Г§вдЫќЫљеМЕФАйЗжБШПЩЕУЕНЕїВщЕФзмШЫЪ§ЃЛдйМЦЫуГіЁА85ЁЋ90ЁБетвЛзщШЫЪ§еМзмВЮШќШЫЪ§ЕФАйЗжБШЃЌШЛКѓгУ1ЗжБ№МѕШЅЦфЫќШ§зщЕФАйЗжБШЕУЕНЁА65ЁЋ70ЁБетвЛзщШЫЪ§еМзмВЮШќШЫЪ§ЕФАйЗжБШЃЌЗжБ№МЦЫуЁА65-70ЁБКЭЁА75-80ЁБетСНзщЕФШЫЪ§ЃЌМДПЩЧѓНтЃЛ
ЃЈ2ЃЉЧѓГіЦНОљЪ§МДПЩХаЖЯЫћФмВЛФмЛёНБЃЛ
ЃЈ3ЃЉЛЪїзДЭМеЙЪОЫљга12жжЕШПЩФмЕФНсЙћЪ§ЃЌдйевГіЧЁКУбЁжа1Фа1ХЎЕФНсЙћЪ§ЃЌШЛКѓИљОнИХТЪЙЋЪНЧѓНтЃЎ
ЃЈ1ЃЉЃЈ2+3ЃЉЁТ10%=50ЃЌ
ЃЈ8+4ЃЉЁТ50=24%ЃЌ
1-10%-24%-36%=30%ЃЌ
50ЁС30%=15ЃЈШЫЃЉЃЌ
ЁрЕУ65ЗжЕФШЫЪ§ЮЊЃК15-8=7ЃЈШЫЃЉЃЌ
50%ЁС36=18ЃЈШЫЃЉЃЌ
ЁрЕУЗжЮЊ80ЗжЕФШЫЪ§ЮЊЃК18-10=8ЃЈШЫЃЉ.
ЃЈ2ЃЉ![]()
![]() ЃЌ
ЃЌ
ЁрЫћПЩвдЛёНБ.
ЃЈ3ЃЉЗЈ1ЃКСаБэШчЯТЃК
Фа1 | Фа2 | ХЎ1 | ХЎ2 | |
Фа1 | ЃЈФа1ЃЌФа2ЃЉ | ЃЈФа1ЃЌХЎ1ЃЉ | ЃЈФа1ЃЌХЎ2ЃЉ | |
Фа2 | ЃЈФа2ЃЌФа1ЃЉ | ЃЈФа2ЃЌХЎ1ЃЉ | ЃЈФа2ЃЌХЎ2ЃЉ | |
ХЎ1 | ЃЈХЎ1ЃЌФа1ЃЉ | ЃЈХЎ1ЃЌФа2ЃЉ | ЃЈХЎ1ЃЌХЎ2ЃЉ | |
ХЎ2 | ЃЈХЎ2ЃЌФа1ЃЉ | ЃЈХЎ2ЃЌФа2ЃЉ | ЃЈХЎ2ЃЌХЎ1ЃЉ |
гЩСаБэЗЈПЩЕУЃЌЫљгаЕШПЩФмЕФНсЙћЙВга12жжЃЌЦфжавЛФавЛХЎга8жж
Ёр![]() .
.
ЗЈ2ЃКЛЪїзДЭМШчЯТЃК
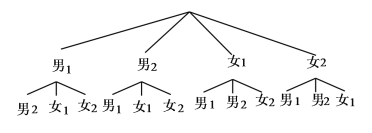
гЩЪїзДЭМПЩЕУЃЌЫљгаЕШПЩФмЕФНсЙћЙВга12жжЃЌЦфжавЛФавЛХЎга8жжЃЌ
Ёр![]() .
.

 НЬбЇСЗаТЭЌВНСЗЯАЯЕСаД№АИ
НЬбЇСЗаТЭЌВНСЗЯАЯЕСаД№АИ ПЮЧАПЮКѓЭЌВНСЗЯАЯЕСаД№АИ
ПЮЧАПЮКѓЭЌВНСЗЯАЯЕСаД№АИ ПЮЬУаЁзївЕЯЕСаД№АИ
ПЮЬУаЁзївЕЯЕСаД№АИ ЛЦИдаЁзДдЊПкЫуЫйЫуСЗЯАВсЯЕСаД№АИ
ЛЦИдаЁзДдЊПкЫуЫйЫуСЗЯАВсЯЕСаД№АИЁОЬтФПЁПСЂЖЈЬјдЖЪЧЬхг§жаПМбЁПМЯюФПжЎвЛЃЌЬхг§ПЮЩЯРЯЪІМЧТМСЫФГЭЌбЇЕФвЛзщСЂЖЈЬјдЖГЩМЈШчБэЃК
ГЩМЈЃЈmЃЉ | 2.3 | 2.4 | 2.5 | 2.4 | 2.4 |
дђЯТСаЙигкетзщЪ§ОнЕФЫЕЗЈЃЌе§ШЗЕФЪЧЃЈЁЁЁЁЃЉ
A.жкЪ§ЪЧ2.3B.ЦНОљЪ§ЪЧ2.4
C.жаЮЛЪ§ЪЧ2.5D.ЗНВюЪЧ0.01