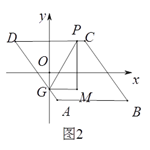题目内容
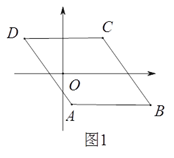
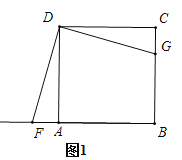
【题目】如图1,将三角板放在正方形![]() 上,使三角板的直角顶点与正方形
上,使三角板的直角顶点与正方形![]() 的顶点
的顶点![]() 重合,三角板的一边交
重合,三角板的一边交![]() 于点
于点![]() ,另一边交
,另一边交![]() 的延长线于点
的延长线于点![]() .
.
(1)求证:![]() ;
;
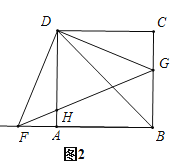
(2)如图2,将三角板绕点![]() 旋转,当
旋转,当![]() 时,连接
时,连接![]() 交
交![]() 于点
于点![]() 求证:
求证:![]() ;
;
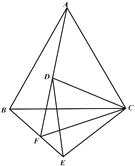
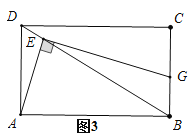
(3)如图3,将“正方形![]() ”改为“矩形
”改为“矩形![]() ”,且将三角板的直角顶点放于对角线
”,且将三角板的直角顶点放于对角线![]() (不与端点重合)上,使三角板的一边经过点
(不与端点重合)上,使三角板的一边经过点![]() ,另一边交
,另一边交![]() 于点
于点![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
(1)根据旋转全等模型利用正方形的性质,由![]() 可证明
可证明![]() ,从而可得结论;
,从而可得结论;
(2)根据正方形性质可知![]() ,结合已知可得
,结合已知可得![]() ;再由(1)可知
;再由(1)可知![]() 是等腰直角三角形可得
是等腰直角三角形可得![]() ,从而证明
,从而证明![]() ,由相似三角形性质即可得出结论;
,由相似三角形性质即可得出结论;
(3)首先过点![]() 作
作![]() ,垂足为
,垂足为![]() ,交AD于M点,由有两角对应相等的三角形相似,证得
,交AD于M点,由有两角对应相等的三角形相似,证得![]() ,根据相似三角形的对应边成比例
,根据相似三角形的对应边成比例![]() ,再由平行可得
,再由平行可得![]() ,由此即可求得答案.
,由此即可求得答案.
(1)证明:∵在正方形ABCD中,![]()
∴![]() ,
,
又∵![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,
 ,
,
∴![]() (ASA),
(ASA),
![]() ;
;
(2)证明 :∵四边形ABCD是正方形,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
由(1)可知![]() ,
,
∴![]() ,
,
∴![]() ,
,
由(1)可知![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
由(1)可知![]() ,
,
∴![]() .
.
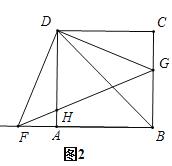
(3)解:如图,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,交AD于M点,
,交AD于M点,
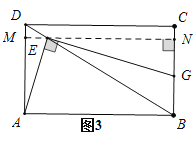
∵四边形ABCD为矩形,
∴![]() ,
,![]() ,
,
∴四边形ABNM是矩形,
∴![]() ,
,![]() ,
,
∴![]()
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
![]()
![]() ,
,
又∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
![]()
![]() ,
,
∵![]()
![]()
![]() .
.

 应用题作业本系列答案
应用题作业本系列答案【题目】小西红柿又叫圣女果,既可以生吃,也可以作为美食原料,营养价值极高,因此深受人们的欢迎,为了解甲、乙两个规模相当的种植基地的小西红柿产量,从这两个种植基地中各随机选取50株小西红柿秧苗进行调查,将得到的数据分类整理成如下统计表:
甲基地每株秧苗收获小西红柿个数统计表:
小西红柿个数x/个 | 25≤x<35 | 35≤x<45 | 45≤x<55 | 55≤x<65 | 65≤x<75 | 75≤x<85 |
秧苗株数/株 | 4 | 8 | 12 | 12 | 10 | 4 |
乙基地每株秧苗收获小西红柿个数统计表:
小西红柿个数 x/个 | 25≤x<35 | 35≤x<45 | 45≤x<55 | 55≤x<65 | 65≤x<75 | 75≤x<85 |
秧苗株数/株 | 9 | 6 | 12 | 10 | 11 | 2 |
(说明:x<45为产量不合格,x≥45为产量合格,其中45≤x<65为产量良好,65≤x<85为产量优秀)
(
(2)某水果商准备在甲、乙两个小西红柿种植基地中选择一个进行合作,若一株秧苗产量优秀可获利13元,产量良好可获利8元,产量不合格亏损5元.以这两个基地的50株秧苗获得的平均利润为决策依据,请你利用所学的统计知识帮该水果商选择与哪个基地进行合作能获得更大利润?并说明理由.
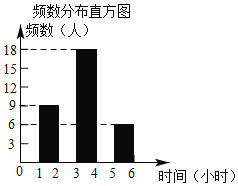
【题目】某中学兴趣小组为了解全校学生星期六和星期日在家使用手机的情况,兴趣小组随机抽取若干名学生,调查他们周末两天的使用手机时间,并根据调查结果绘制了下面两幅不完整的统计表和统计图.根据图表信息,解答下列问题:
阅读时间 (小时) | 频数 (人) | 频率 |
1≤x<2 | 9 | 0.15 |
2≤x<3 | a | m |
3≤x<4 | 18 | 0.3 |
4≤x<5 | 12 | n |
5≤x<6 | 6 | 0.1 |
合计 | b | 1 |
(1)填空:a= ,b= ,m= ,n= :
(2)将频数分布直方图补充完整;
(3)这个中学的学生共有1200人,根据上面信息来估算全校学生中周末两天使用手机时间不低于4小时的学生大约有多少人?