题目内容
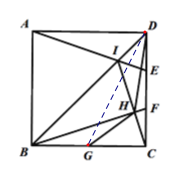
【题目】如图,E,F是正方形ABCD的边CD上两个动点,满足DE=CF.连接AE交BD于点I,连接BF交CI于点H,G为BC边上的中点.若正方形的边长为4,则线段DH长度的最小值是__________.

【答案】![]() -2
-2
【解析】
易证ADEBCF,得∠DAE=∠CBF,由A,C关于BD轴对称,得∠DAE=∠DCI,从而得∠CBF=∠DCI,进而得∠BHC=90°,结合G为BC边上的中点,得GH=2,连接DG,得DG=![]() ,根据三角形三边长关系,即可得到答案.
,根据三角形三边长关系,即可得到答案.
∵在正方形ABCD中,AD=BC,∠ADE=∠BCF=90°,
又∵DE=CF,
∴ADEBCF(ASA),
∴∠DAE=∠CBF,
∵A,C关于BD轴对称,
∴∠DAE=∠DCI,
∴∠CBF=∠DCI,
∴∠DCI+∠BCH=∠CBF+∠BCH=90°,
∴∠BHC=180°-(∠CBF+∠BCH)=180°-90°=90°,
∵G为BC边上的中点,
∴GH=![]() BC=2,
BC=2,
连接DG,则DG=![]() ,
,
∵在DHG中,DH>DG-GH,当且进当D,H,G三点共线时,DH=DG-GH=![]() -2,
-2,
∴线段DH长度的最小值是:![]() -2.
-2.
故答案是:![]() -2.
-2.

练习册系列答案
相关题目